आपलोगों ने fundamental maths के पोस्ट को बहुत सारा प्यार दिये इसके लिए आप सभी को बहुत-बहुत धन्यवाद । fundamental maths (बेसिक गणित) में और भी कुछ महत्वपूर्ण चैप्टर है ,जिसको पढ़ना बहुत ही जरूरी है। इसलिए आज हम इस maths में “अभाज्य गुणनखंड ,गुणज ,HCF , LCMलेकर आया हूँ। इसको डिटेल से पढ़ेंगे ।
● गुणनखंड क्या है ( what is factor)
सबसे पहले जान लेते हैं गुणनखंड का मतलब क्या होता है ? (गुणनखंड- गुना का खंड या टुकड़ा) जैसे 8 का गुणनखंड क्या होगा ? 4×2 , 8 का गुणनखंड होगा। क्योंकि 8 को गुना के फॉर्म में लिखा है। 4×2 = 8 ,या तो आप 8 लिखे या आप 4×2 लिखें एक ही बात होगा। 8 का गुणनखंड 4 होगा। 8 का गुणनखंड 2 भी होगा ।

परिभाषा :- किसी संख्या का गुणनखंड वह संख्या है जिससे मूल संख्या में पूरा-पूरा भाग लग जाए।
क्या 8 को सिर्फ 4×2 के खंड में ही लिख सकते हैं उसके अलावा किसी खंड में नहीं लिखा जाएगा। ऐसा बिल्कुल भी नहीं है। 2×2×2 , 8×1 और 4×2 ये 8 को गुणनखंड के रूप में लिखने का अलग-अलग तरीका है।
किसी भी संख्या का गुणनखंड निकालने का एक तरीका होता है। लेकिन उससे पहले अगर आप विभाज्यता का नियम नहीं जानते हैं तो आप बड़ी संख्या का गुणनखंड नहीं निकाल पाएंगे अगर निकाल भी लेंगे तो बहुत समय लगेगा। जैसे हम 20 का गुणनखंड निकलते हैं।
20 = 4×5 (हाँ ,4 और 5 ,20 का गुणनखंड है )
20 = 2×10 (2 और 10 भी 20 गुणनखंड है)
20 = 20×1 (20 और 1 भी 20 गुणनखंड है )
ये छोटी संख्या है तो मैंने आराम से निकाल दिया । लेकिन अगर पूछा जाए । क्या 1280 संख्या का एक जोड़े गुणनखंड में से एक 4 होगा या नहीं ?
| Fundamental Maths Topic (बेसिक गणित का टॉपिक ) 1.संख्या और अंक (Number and Digit) 2. संख्या रेखा (Number Line) 3.संख्याओं की परिभाषा (Definition of Numbers) 4.विभाज्यता का नियम (Rule of Divisibility) 5.भारतीय और अंतरराष्ट्रीय संख्या पद्धति (Indian and International Number System ) 6.भिन्न ,अनुपात और प्रतिशत (Fraction, Ratio and Percentage) 7.ऐकिक नियम (Unitary method) 8.अभाज्य गुणनखंड, गुणज, अपवर्तक, समापवर्तक, अपवर्त्य, समापवर्त्य, HCF, LCM 9.घातांक और घात (Exponent and Power) 10.लाभ और हानि (Profit and Loss) 11.दशमलव (Decimals) 12.आकृतियों, कोणों, रेखाओं (Shapes, Angles, Lines ) 13.वर्गमूल (Square root) 14.घनमूल (cube root) 15.प्राकृतिक संख्या (Natural Number) 16.पूर्ण संख्या ( Whole Number) 17.पूर्णांक (Integers) 18.क्षेत्रमिति (Mensuration) 19.अपवर्तक (Factor) 20.अपवर्त्य (Multiple) 21.गुणनखंड (Factorisation) 22.पूर्ण संख्या और पूर्णांक में अंतर 23.प्रतिशत (Percentage) |
अगर आप विभाज्यता का नियम जानते हैं तो इसका उत्तर देना बहुत आसान है। अगर यह संख्या 4 से विभाजित होगा तो 4 इसका उत्तर होगा। लेकिन एक दूसरा तरीका भी है जिसे मैंने नीचे बना कर दिखाया है।
| 2 | 1280 | 1280 में 2 से भाग देने पर 640 भागफल हुआ। |
| 2 | 640 | फिर 640 में 2 से भाग देने पर भगफल 320 हुआ। |
| 2 | 320 | फिर 320 में 2 से भाग देने पर भगफल 160 हुआ। |
| 2 | 160 | फिर 160 में 2 से भाग देने पर भगफल 80 हुआ। |
| 2 | 80 | फिर 80 में 2 से भाग देने पर भगफल 40 हुआ। |
| 2 | 40 | फिर 40 में 2 से भाग देने पर भगफल 20 हुआ। |
| 2 | 20 | फिर 20 में 2 से भाग देने पर भगफल 10 हुआ। |
| 2 | 10 | फिर 10 में 2 से भाग देने पर भगफल 5 हुआ। |
| 5 | 5 | फिर 5 में 5 से भाग देने पर भगफल 1 हुआ। |
| 1 |

इस तरीका से किसी भी संख्या का गुणनखंड निकाला जा सकता है। मैंने सबसे पहले 2 से भाग दिया। उसके बाद 2 से भाग देता रहा जब तक कि 2 से नहीं लगे।
लेकिन अगर गुणनखंड निकाल रहें हैं तो आप किसी भी संख्या से भाग देने के लिए स्वतंत्र है। वहीं अभाज्य गुणनखंड में ये स्वतंत्रता नहीं रहती है। अभाज्य गुणनखंड के बारे में आगे बताया गया है।
● योज्यखंड क्या है
क्या आपने कभी सोचा है और किसी संख्या के गुणन के खंड (गुणनखंड) निकाल सकते हैं तो जोड़ खंड (योज्य खंड) भी हो सकता है। लेकिन योज्य खंड के बारे में चर्चा नहीं होती है क्योंकि इसकी कभी जरूरत नहीं हुई ।
जैसे किसी संख्या का गुणनखंड निकलते हैं उसी तरह से योज्य-खंड भी निकाला जा सकता है। जैसे 20 का योज्य-खंड 1+19, 2+18, 3+17, 4+16, 5+15, 6+14, 7+13, 8+12, 9+11, 10+10.
इसमें सम योज्य खंड ,विषम योज्य खंड ,अभाज्य योज्य खंड, भाज्य योज्य खंड इत्यादि हो सकता है ।
● अभाज्य गुणनखंड क्या है (what is Prime Factorisation)
अभाज्य गुणनखंड किसी संख्या का ऐसा गुणनखंड होता है जिसमें सिर्फ अभाज्य संख्या हो। कोई भी संख्या का अभाज्य गुणनखंड निकाला जा सकता है।
जैसे ऊपर मैंने 1280 का गुणनखंड निकाला है वह एक अभाज्य गुणनखंड है।
1280 = 2×2×2×2×2×2×2×2×5 इसमें सभी अभाज्य संख्या है। इसलिए ये 1280 का अभाज्य गुणनखंड कहलायेगा।
अभाज्य गुणनखंड का नियम :-
- सबसे पहले देखते हैं संख्या कौन-सी सबसे छोटी अभाज्य संख्या से विभाजित होता है। फिर उसके भगफल को नीचे लिखते हैं।
- फिर भगफल को उसी तरह से किसी अभाज्य संख्या से भाग देते हैं और फिर उसे नीचे लिखते हैं।
- ऐसा तबतक करते हैं जब तक अंतिम भगफल अभाज्य संख्या प्राप्त न हो जाये।
- अब सभी अभाज्य भाजक और अंतिम अभाज्य भगफल को गुना करके लिखते हैं और गुण करके वह संख्या प्राप्त हो जाती है।
● अपवर्तक
जैसे एक कोई संख्या 21 लेते हैं। अब 21 को कौन-कौन सी संख्या पूर्ण विभाजित करेगी। 1,3,7 और 21 इतनी ही संख्या से 21 पूर्ण विभाजित होगी। इसलिए 1,3,7,और 21 को 21 का अपवर्तक कहेंगे।
परिभाषा :- किसी संख्या को पूर्ण विभाजित करने वाली सभी संख्याएं। उस संख्या का अपवर्तक कहलाता है।
12 का अपवर्तक :-
| संख्या | अपवर्तक |
| 1 | 1 |
| 2 | 1 और 2 |
| 3 | 1 और 3 |
| 4 | 1,2 और 4 |
| 5 | 1 और 5 |
| 6 | 1,2,3 और 6 |
| 7 | 1 और 7 |
| 8 | 1,2,4 और 8 |
| 9 | 1,3 और 9 |
| 10 | 1,2,5 और 10 |
| 11 | 1 और 11 |
| 12 | 1,2,3,4,6 और 12 |
| 13 | 1 और 13 |
| 14 | 1,2,7 और 14 |
| 15 | 1,3,5 और 15 |
| 16 | 1,2,4,8 और 16 |
● समापवर्तक
अपवर्तक में सिर्फ एक संख्या लेते हैं। लेकिन समापवर्तक अगर निकाल रहें हैं तो कम से कम दो संख्या तो होना ही चाहिए।
परिभाषा :- किसी दो या दो से अधिक संख्याओं के अपवर्तकों में Common अपवर्तक , समापवर्तक कहलाता है।
उदाहरण :- 12 और 20 का समापवर्तक निकालें ।
हल :- सबसे पहले 12 और 20 का अपवर्तक निकलना होगा।
12 का अपवर्तक :- 1, 2, 3, 4, 6 और 12
20 का अपवर्तक :- 1, 2, 4, 5, 10 और 20
12 और 20 का समापवर्तक :- 1, 2 और 4 होगा । 12 और 20 के अपवर्तकों में सिर्फ 1, 2 और 4 अपवर्तक ही common थे।
● महत्तम समापवर्तक (Highest Common Factor – HCF )
किसी भी समापवर्तक में जो सबसे बड़ा (महत्तम) समापवर्तक होगा वही महत्तम समापवर्तक कहलाता है।
12 और 20 का समापवर्तक :- 1, 2 और 4 होगा ।
तो महत्तम समापवर्तक ( HCF) :- 4 होगा।
वैसे HCF निकलने के लिए तीन नियम होते हैं जो निम्नलिखित हैं ।
- भाग विधि द्वारा HCF,
- गुणनखंड विधि द्वारा HCF और
- अपवर्तक विधि द्वारा HCF
1.भाग विधि द्वारा HCF
एक उदाहरण लेकर हम आपको समझते हैं। 15 और 200 का HCF भाग विधि द्वारा निकले।
भाग विधि द्वारा HCF निकालने के लिए सबसे छोटी संख्या से उससे बड़ी संख्या में भाग दिया जाता है। जो शेषफल होता है। उस शेषफल से फिर भाजक में भाग दिया जाता है। यह सिलसिला तबतक करते हैं जबतक की शेषफल शून्य न हो जाये।
उदाहरण : 15 और 200 का HCF भाग विधि द्वारा निकालें ।
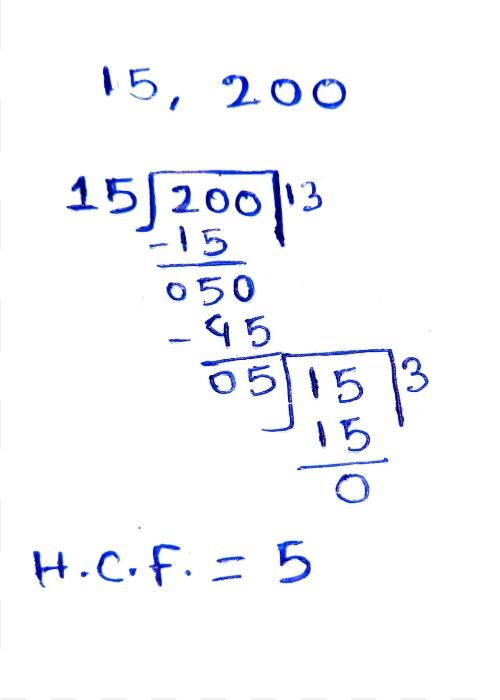
15 और 200 का HCF भाग विधि द्वारा निकालने के लिए सबसे छोटी संख्या 15 से 200 में भाग दिये, शेषफल 5 हुआ इस शेषफल से भाजक 15 में फिर भाग दिए अब शेषफल 0 हो गया। अब जिस संख्या से अंतिम बार भाग दिया जाता है वही HCF होता है। यहाँ HCF 5 हुआ ।
उदाहरण : 154, 118 और 138 का HCF भाग विधि द्वारा निकालें ।
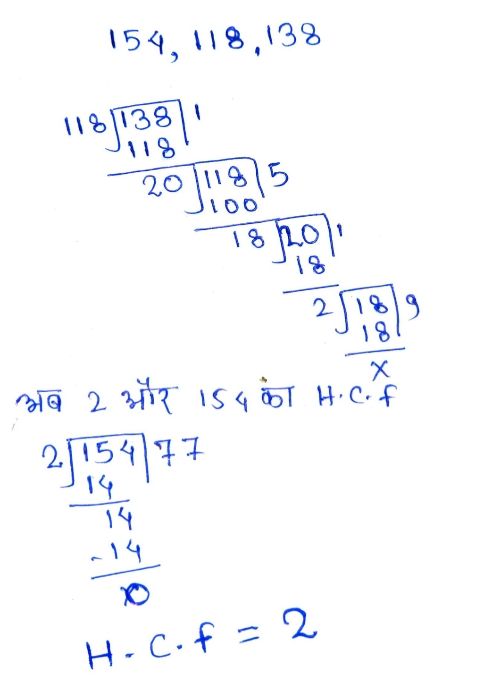
अगर दो या दो से अधिक संख्याओं को एक साथ भाग विधि से HCF निकालने कहा जाए तो सबसे पहले दोसबसे छोटी संख्या में भाग दिया जाता है।
जैसा मैंने 154, 118 और 138 का HCF निकालने में किया है। सबसे पहले 118 और 154 का HCF निकाला गया है।
उसके बाद इन दोनों के HCF से बचे संख्या का HCF निकाला गया । मतलब 2 और 154 का HCF अब इन दोनों संख्याओं का HCF 2 हुआ । इसलिए 154, 118 और 138 का HCF 2 होगा ।
2.गुणनखंड विधि द्वारा HCF
HCF निकलने का दूसरा विधि गुणनखंड के द्वारा होता है। इस विधि में सभी संख्याओं का गुणनखंड निकाला जाता है। उसके बाद सभी संख्याओं के गुणनखंड के common संख्याओं को गुना कर दिया जाता है वही HCF होता है।
उदाहरण : 16 और 20 का HCF गुणनखंड विधि से निकालें ।
हल :- सबसे पहले 16 और 20 का अभाज्य गुणनखंड निकलेंगे ।
16 का अभाज्य गुणनखंड = 2 × 2 × 2 × 2 × 1
20 का अभाज्य गुणनखंड = 2 × 2 × 5 × 1
अब 16 और 20 का HCF = 2 × 2 × 1 = 4 होगा।
[ 16 और 20 के गुणनखंड में 2 × 2 × 1 कॉमन है इसलिए यही HCF होगा । ]
उदाहरण : 48, 25 और 23 का HCF गुणनखंड विधि से निकालें ।
हल :- सबसे पहले 48, 25 और 23 का अभाज्य गुणनखंड निकलेंगे ।
48 का गुणनखंड = 2 × 2 × 2 × 2 × 3 × 1
25 का गुणनखंड = 5 × 5 × 1
23 का गुणनखंड = 23 × 1
अब , 48 ,25 और 23 का HCF = 1 होगा। क्योंकि सभी संख्याओं के गुणनखंड का कॉमन सिर्फ 1 ही है।
3.अपवर्तक विधि द्वारा HCF
HCF निकलने का एक और तरीका अपवर्तक विधि का है। इस विधि में सबसे पहले संख्याओं के अपवर्तक निकालना होगा है । उसके बाद समापवर्तक निकलते हैं। उसके बाद जो सबसे बड़ा समापवर्तक होता है। वही महत्तम समापवर्तक (HCF ) होता है।
उदाहरण : 14 और 16 का अपवर्तक विधि से HCF निकालें ।
हल : सबसे पहले 14 और 16 का अपवर्तक निकलेंगे।
14 का अपवर्तक – 1, 2, 7 और 14
16 का अपवर्तक – 1, 2, 4, 8 और 16
14 और 16 का समापवर्तक – 1 और 2 होगा।
इसलिए 14 और 16 का महत्तम समापवर्तक (HCF) 2 होगा ।
उदाहरण : 20, 24 और 48 का अपवर्तक विधि से HCF निकालें ।
हल : सबसे पहले 20, 24 और 48 का अपवर्तक निकलेंगे ।
20 का अपवर्तक – 1, 2, 4, 5, 10 और 20
24 का अपवर्तक – 1, 2, 3, 4, 6, 8, 12 और 24
48 का अपवर्तक – 1, 2, 3, 4, 6, 8, 12, 16, 24 और 48
20, 24 और 48 का समापवर्तक – 1, 2 और 4 होगा।
इसलिए 20, 24 और 48 का महत्तम समापवर्तक (HCF) 4 होगा ।
● गुणज /अपर्वत्य (Multiple)
किसी संख्या का गुणनखंड एक सीमित संख्या ही होगा लेकिन किसी सांख्य का गुणज अनन्त हो सकता है।
जैसे 8 का गुणज (अपर्वत्य) होगा,
8×1 = 8,
8×2 = 16,
8×3 = 24,
8×4 = 32,
8×5 = 40,
8×6 = 48,
8×7 = 56,
8×8 = 64,
8×9 = 72,
…….
8 का गुणज (अपर्वत्य) 8,16,24,32,40,48,56,64,72…….,
उदाहरण : 29 का प्रथम 5 गुणज निकले।
29×1 = 29,
29×2 = 58,
29×3 = 87,
29×4 = 116,
29×5 = 145,
29 का प्रथम 5 गुणज 29, 58, 87, 116 और 145 होगा।
● समापवर्त्य
कम से कम दो या दो से अधिक संख्याओं का अपर्वत्य (गुणज) निकाल कर सभी संख्याओं के common अपर्वत्य ही समापवर्त्य कहलाता है।
उदाहरण :- 2 और 4 का समापवर्त्य निकले।
हल:- सबसे पहले 2 और 4 का अपर्वत्य निकालना होगा।
2 का अपर्वत्य – 2, 4, 6, 8, 10, 12, 14, 16, 18, 20………..
4 का अपर्वत्य – 4, 8,12, 16, 20, 24, 28, 32, 36, 40…..
अब 2 और 4 का समापवर्त्य – 4, 8,12, 16, 20, 24, 28….
● LCM (लघुत्तम समापवर्त्य )
सबसे छोटी समापवर्त्य को लघुत्तम समापवर्त्य (LCM) कहा जाता है।
उदाहरण : 6 और 8 का लघुत्तम समापवर्त्य निकालें ।
हल:- सबसे पहले 6 और 8 का अपर्वत्य निकलते हैं।
6 का अपर्वत्य – 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72…..
8 का अपर्वत्य – 8, 16, 24, 32, 40, 48, 56, 64, 72, 80…
6 और 8 का समापवर्त्य – 24, 48, 72 …
6 और 8 का लघुत्तम समापवर्त्य – 24 होगा ।
LCM निकालने का भी तीन विधि होता है।
- भाग विधि द्वारा LCM,
- गुणनखंड विधि द्वारा LCM और
- अपर्वत्य विधि द्वारा LCM
1.भाग विधि द्वारा LCM
भाग विधि से LCM निकालना बहुत आसान है।
नियम :-
- सबसे पहले जो भी संख्याएँ हैं उसे एक लाइन में लिख दिया जाता है।
- उसके बाद जिस संख्या से कम से कम दो संख्यां पूर्ण विभाजित होता है, उससे भाग दिया जाता है।
- नीचे में भाग देने पर जो भागफल होता है उस संख्या के नीचे लिखा जाता है और जिस संख्या में भाग नहीं लगता है उसे वैसे ही उतार दिया जाता है।
- फिर उसी तरह से नीचे लिखे संख्या को देखा जाता है कि कौन सी संख्या से पूर्ण विभाजित होगा।
- ऐसा तबतक किया जाता है जबतक कि किसी दो संख्याओं में किसी एक संख्या से भाग लग जाये।
- नीचे उदाहरण से समझ सकते हैं।
उदाहरण : 20, 50, 34 और 18 का LCM निकालें।
हल :
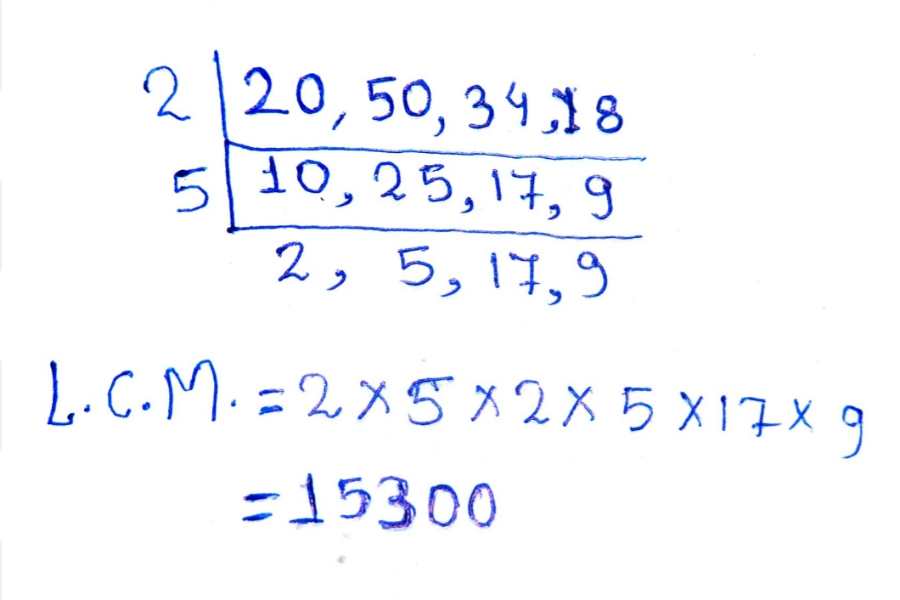
2.गुणनखंड विधि द्वारा LCM
गुणनखंड विधि से LCM निकलने के लिए।
- सबसे पहले संख्याओं का गुणनखंड निकालना पड़ता है।
- उसके बाद सभी संख्याओं के गुणनखंड में से कॉमन संख्याओं को एक बार लिखा जाता है।
- इस कॉमन संख्या के साथ बचे सभी संख्याओं का गुण किया जाता है।
- सभी संख्याओं का गुणनफल ही इन सभी संख्याओं का LCM कहलाता है।
उदाहरण : 26, 48, 20 और 15 का LCM गुणनखंड विधि से निकालें।
हल :- सबसे पहले 26, 48, 20 और 15 का गुणनखंड निकालना पड़ेगा।
26 का गुणनखंड = 2 × 13
48 का गुणनखंड = 2 × 2 × 2 × 2 × 3
20 का गुणनखंड = 2 × 2 × 5
15 का गुणनखंड = 3 × 5
26, 48, 20 और 15 का LCM = 2 × 2 × 3 × 5 × 2 × 2 × 13 = 3120
3.अपर्वत्य विधि द्वारा LCM
अपर्वत्य विधि से LCM निकालने के लिए ।
- सबसे पहले सभी संख्याओं का अपर्वत्य ( गुणज ) निकलना पड़ता है।
- उसके बाद सभी संख्यायों का समापवर्त्य निकलना पड़ता है।
- अंतिम में जो सबसे छोटा समापवर्त्य होगा वही LCM कहलाता है।
उदाहरण : 20, 6, 10 और 15 का LCM अपर्वत्य विधि से निकालें ।
हल : सबसे पहले 20, 6, 10 और 15 का अपर्वत्य निकालना पड़ेगा।
20 का अपर्वत्य – 20, 40, 60, 80, 100, 120……
6 का अपर्वत्य – 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, …120, ……
10 का अपर्वत्य – 10, 20, 30, 40, 50, 60, 70, 80, 90, 100..,120, …..
15 का अपर्वत्य – 15, 30, 45, 60, 75, 90, 105, 120 …….
20, 6, 10, 15 का समापवर्त्य – 60, 120 ……
20, 6, 10, 15 का LCM होगा – 60