संख्या (number) क्या होता है ? इसके बारे में मैंने पहले ही बता दिया है । इस पोस्ट में सभी संख्याओं की परिभाषा बहुत ही आसान भाषा में डिटेल से बताया है। fundamental maths (बेसिक गणित ) का एक महत्वपूर्ण टॉपिक है ।
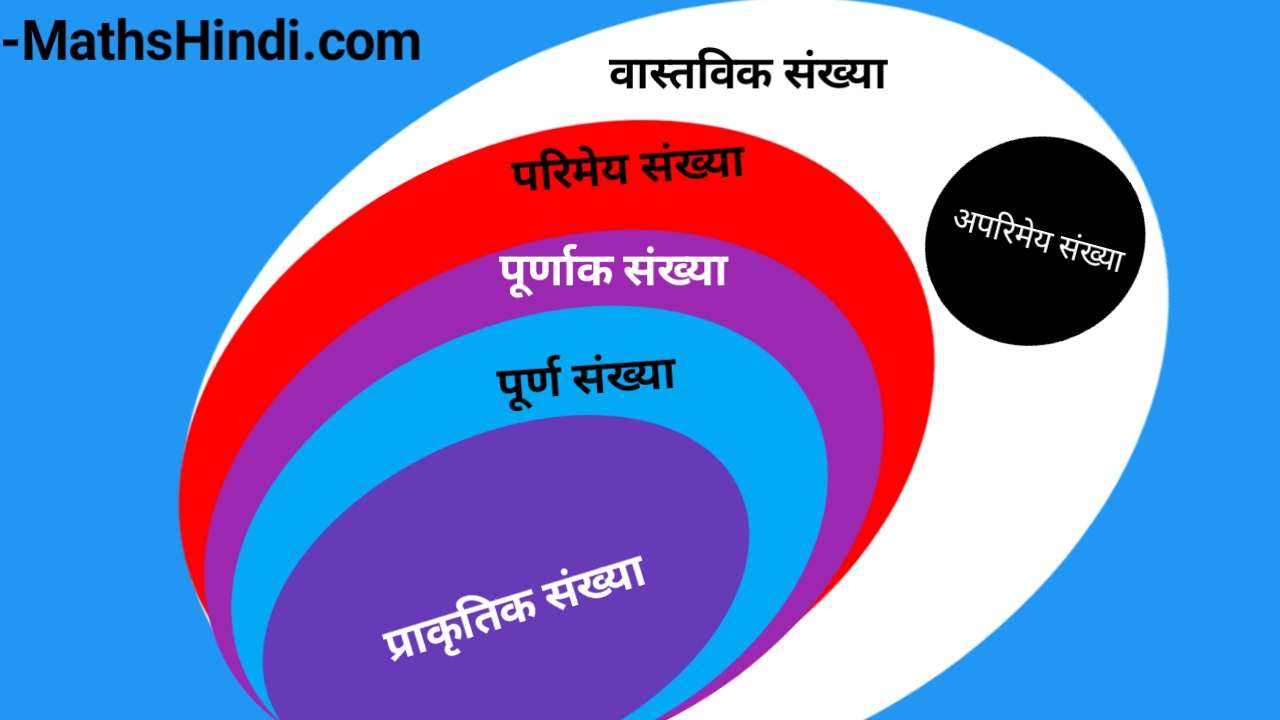
1. प्राकृतिक संख्या (Natural Number )
प्राकृतिक संख्या का परिभाषा याद रखने की जरूरत नहीं है। संख्या रेखा पर सभी धनात्मक पूर्णक को प्राकृतिक संख्या कहा जाता है।
……….-3,-2,-1,0,1,2,3,4,5……….
प्राकृतिक संख्या की शुरुआत 1 से होती है और अनन्त तक जाता है।
2. पूर्ण संख्या (Whole Number )
पूर्ण संख्या का परिवार प्राकृतिक संख्या के परिवार से बड़ा होता है । पूर्ण संख्या की शुरुआत 0 से होती है और अनन्त तक जाती है। इसलिए कह सकते हैं सभी प्राकृतिक संख्या पूर्ण संख्या कहलाती है, लेकिन सभी पूर्ण संख्या प्राकृतिक संख्या नहीं होती है।
……….-3,-2,-1,0,1,2,3,4,5……….
3. धनात्मक संख्या (Positive Number )
सभी प्राकृतिक संख्या को धनात्मक संख्या कहा जाता है। धनात्मक संख्या की शुरुआत 1 से होती है और अनन्त तक जाती है।
……….-3,-2,-1,0,1,2,3,4,5……….
4. ऋणात्मक संख्या (Negetive Number )
संख्या रेखा पर 0 को छोड़कर बायाँ साइड जो भी संख्याएँ होती है वह सभी ऋणात्मक संख्या कहलाती है। जैसे -1,-2,-3,-4…..
……….-3,-2,-1,0,1,2,3,4,5……….
5. पूर्णांक संख्या (Integers)
यहाँ बहुत अच्छे से ध्यान रखना चाहिए कि पूर्ण संख्या और पूर्णांक संख्या में बहुत अंतर होता है।
सभी धनात्मक संख्या ,ऋणात्मक संख्या और शून्य को पूर्णक संख्या कहा जाता है । जैसे -5,-8,-108,0,657,8,2… ये सभी संख्याएँ पूर्णांक संख्या कहलाएगी। लेकिन 5/2 ,-2/3, -3.2 ,8.1 … ऐसी संख्याएँ पूर्णांक नहीं कहलाती है।
6. परिमेय संख्या (Rational Number)
परिमेय संख्या को अच्छे से समझना जरूरी है । परिमेय संख्या में बहुत सारी संख्याएँ आती है। इसको पहचानने के नियम है ।
वैसी संख्या जो भिन्न के रूप में लिखा जा सकें लेकिन उस भिन्न का हर, शून्य के बराबर नहीं हो वह परिमेय संख्या कहलाती है।
या , वैसी संख्या जो p/q के रूप में लिखा जा सकें लेकिन q≠0 हो ,वह परिमेय संख्या कहलाती है।
जैसे :- 5/2 ,-6/4 , 3.5, 6,0, 3….. ऐसी सभी संख्याएँ परिमेय संख्याएँ हैं।
5/2 – p/q के रूप में लिखा हुआ है क्योंकि यहाँ p=5 और q=2 है।
-6/4 – p/q के रूप में लिखा हुआ है क्योंकि यहाँ p=-6 और q=4 है।
3.5 – p/q के रूप में लिखा हुआ है क्योंकि इसे हम p/q के रूप में लिख सकते हैं
3.5= 35/10 यहाँ p=35 और q= 10 है।
6 – p/q के रूप में लिखा हुआ है क्योंकि यहाँ 6 को 6/1 लिख सकते हैं जिससे p=6 और q=1 होगा ।
0 – p/q के रूप में लिखा हुआ है क्योंकि यहाँ 0 को भी 0/1 लिख सकते हैं जिससे p=0 और q= 1 होगा ।
नोट :- शून्य एक परिमेय संख्या हैं ।
परिमेय संख्या के परिभाषा में यह नहीं लिखा है कि p=0 नहीं होना चाहिए । p=0 (अंस) हो सकता है लेकिन q=0 (हर) नहीं होना चाहिए।
7. अपरिमेय संख्या (Irrational Number)
जो संख्या भिन्न के रूप में नहीं लिखा जाए उसे अपरिमेय संख्या कहा जाता है ।
या जो संख्या p/q के रूप में नहीं लिखा जा सके । इसके मतलब यह नहीं होता है कि परिमेय संख्या का उल्टा अपरिमेय संख्या में q= 0 होता है। ऐसा बिल्कुल भी नहीं होता है । वैसे वास्तविक जीवन में दो तरह की ही संख्याएँ होती है परिमेय संख्या और अपरिमेय संख्या ।
अपरिमेय संख्या अभी भी आप नहीं समझे होंगे कोई बात नहीं डिटेल से समझ लीजिए फिर इसे याद करने की झंझट ही नहीं होगी। जब हम किसी भी भिन्न को दशमलव संख्या में बदलते हैं तब देखते होंगे कि कुछ भिन्न को बदलने के बाद दशमलव के बाद एक ही संख्या बार-बार आती है (3.66666….) या कुछ संख्याओं का पुनरावृत्ति होती है (7.187618751875…..)। ऐसी संख्या परिमेय संख्या ही कहलाती है लेकिन जब दशमलव के बाद कुछ अलग ढंग से पुनरावृत्ति होती है जैसे 23.101001000100001… इस तरह की संख्याएँ अपरिमेय संख्या होती है ।
रूट के अंदर सभी अभाज्य संख्या अपरिमेय संख्या ही होती है । √2,√3,√5,√7,√11,…
π भी अपरिमेय संख्या कहलाती है । π=3.14159…
8. वास्तविक संख्या (Real Number )
वास्तविक संख्या का परिभाषा बहुत आसान है । जो भी संख्या है सभी वास्तविक संख्या है ।
सभी परिमेय और अपरिमेय संख्याओं को वास्तविक संख्या कहा जाता है।
9. अवास्तविक संख्या (Unreal Number, Imaginary Number )
वैसे आपके जानकारी के लिए बता दूं अवास्तविक संख्या का वास्तविक जीवन में उपयोग नहीं होता है। इस संख्या की परिभाषा आसान है । वैसी संख्या जो वास्तविक संख्या नहीं है वैसी संख्या को अवास्तविक संख्या कहते हैं।
सभी नेगेटिव रूट संख्या को अवास्तविक संख्या , कहते हैं।
उदाहरण :- √-3 , √-1 etc.
जब कोई मेनस (-) रूट के अंदर हो और वह रूट से बाहर नहीं निकल सकें वह अवास्तविक संख्या कहलाती है । √-1 को i माना जाता है. i का मतलब imagenery होता है। जैसे √-3 को √-1×3 लिख सकते हैं । इसलिए इसे √3i लिख सकते हैं।
हम i को ऐसे देख सकते हैं
√-1=i
-1=i²
जब वास्तविक संख्या और imagenery नंबर को एक साथ रखा जाता है तो वह complex number कहलाता है।
जैसे 8+3i
10. सम संख्या (Even Number )
सम संख्या का अलग-अलग परिभाषा हो सकता है । जैसे जिस संख्या को दो पूर्ण बराबर भाग में बांटा जा सकें वह सम संख्या कहलाती है ।
या , जिस संख्या को 2 से भाग देने पर पूरा-पूरा (पूर्ण) विभाजित हो जाये वह सम संख्या कहलाता है।
2,4,6,8,10,12,14,16,18…
- अगर ऋणात्मक सम संख्या कहा जाए तो इसका मतलब -2, -4,-6, -8, -10, -12…. होगा।
- अगर धनात्मक सम संख्या कहा जाए तो इसका मतलब 2, 4, 6, 8, 10, 12…. होगा।
प्रश्न 1 : अगर पहला सम संख्या x है तो इसके आगे लगातार सम संख्या क्या होगी ?
पहली सम संख्या x है तो इसके बाद लगतार सम संख्या आराम से निकला जा सकता है ।
x,
x+2,
x+2+2,
x+2+2+2,
x+2+2+2+2,
x+2+2+2+2+2, ….
इसको लिख सकते हैं :- x, x+2, x+4, x+6, x+8, x+10…….
अगर x के जगह पर 2 मान रखा जाए तो लगातार संख्या बनेगा 2, 4, 6, 8, 10, 12, ..
प्रश्न 2 : क्या 0 (शून्य ) एक सम संख्या है ?
हाँ ,0 (शून्य) एक सम संख्या है । क्योंकि 0 में 2 से भाग देने पर पूर्ण विभाजित हो जाता है। 0÷2 = 0.
11. विषम संख्या (Odd Number)
विषम संख्या सम संख्या का उल्टा होता है । जिस संख्या को दो पूर्ण बराबर भाग ने बांटा न जा सके ।
या, किसी संख्या को 2 से भाग देने पर पूर्ण विभाजित न हो उसे विषम संख्या कहते है।
1, 3, 5, 7, 9, 11, 13, 15, ………
- अगर ऋणात्मक विषम संख्या कहा जाए तो इसका मतलब -1, -3,-5, -7, -9, -11…. होगा।
- अगर धनात्मक विषम संख्या कहा जाए तो इसका मतलब 1, 4, 6, 8, 10, 12…. होगा।
प्रश्न 1 : अगर पहला विषम संख्या y है तो इसके आगे लगातार विषम संख्या क्या होगी ?
पहली विषम संख्या y है तो इसके बाद लगतार विषम संख्या आराम से निकला जा सकता है ।
y,
y+2,
y+2+2,
y+2+2+2,
y+2+2+2+2,
y+2+2+2+2+2, …..
इसको लिख सकते हैं :- y, y+2, y+4, y+6, y+8, y+10…….
अगर y के जगह पर 1 मान रखा जाए तो लगातार संख्या बनेगा 1, 3, 5, 7, 9, 11, ..
12. भाज्य संख्या (Composite Number)
वैसी संख्या जो स्वयं और 1 के अलावा किसी दूसरे संख्या से भी पूर्ण विभाजित हो वह भाज्य संख्या कहलाती है।
जैसे :- 9 एक संख्या है। लेकिन यह भाज्य है या नहीं चलिये देखते हैं । 9 संख्या 1 और 9 से पूर्ण विभाजित हो ही जायेगा । आप भाग देकर देख लीजिए । क्या 1 और 9 के अलावा किसी दूसरे संख्या से भी विभाज्य होगा या नही । हाँ ,9 एक और संख्या 3 से पूर्ण विभाज्य होता है । इसलिय 9 एक भाज्य संख्या है ।
| संख्या | विभाजित करने वाली संख्याएँ | भाज्य संख्या है या नहीं |
| 2 | 1,2 | भाज्य संख्या नहीं है। |
| 3 | 1,3 | भाज्य संख्या नहीं है। |
| 4 | 1,2,4 | भाज्य संख्या है। |
| 5 | 1,5 | भाज्य संख्या नहीं है। |
| 6 | 1,2,3,6 | भाज्य संख्या है। |
| 7 | 1,7 | भाज्य संख्या नहीं है। |
| 8 | 1,2,4,8 | भाज्य संख्या है। |
| 9 | 1,3,9 | भाज्य संख्या है। |
| 10 | 1,2,5,10 | भाज्य संख्या है। |
13. अभाज्य संख्या (Prime Number )
वैसी संख्या जो सिर्फ 1 और स्वयं से ही पूर्ण विभाजित हो वह अभाज्य संख्या कहलाती है।
| संख्या | विभाजित करने वाली संख्याएँ | अभाज्य संख्या है या नहीं |
| 2 | 1,2 | अभाज्य संख्या है। |
| 3 | 1,3 | अभाज्य संख्या है। |
| 4 | 1,2,4 | अभाज्य संख्या नहीं है। |
| 5 | 1,5 | अभाज्य संख्या है। |
| 6 | 1,2,3,6 | अभाज्य संख्या नहीं है। |
| 7 | 1,7 | अभाज्य संख्या है। |
| 8 | 1,2,4,8 | अभाज्य संख्या नहीं है। |
| 9 | 1,3,9 | अभाज्य संख्या नहीं है। |
| 10 | 1,2,5,10 | अभाज्य संख्या नहीं है। |