त्रिकोणमिति का परिचय (Introduction of Trigonometry) Class 10 maths Chapter 8

त्रिकोणमिति का परिचय (Introduction of Trigonometry) Class 10 के NCERT गणित का चैप्टर नंबर 8 है। इस चैप्टर में हम त्रिकोणमति का बेसिक जानेगे। चलिए शुरू करते हैं। त्रिकोणमिति चैप्टर में समकोण त्रिभुज के बारे में पढ़ा जाता है।

इस चैप्टर को पढ़ने के बाद आप किसी भी ईमारत या मजिल का ऊंचाई नीचे से ही माप सकते हैं। जैसे एक ईमारत कितनी ऊँची है इसको निकलने के लिए आपको कुछ नहीं करना है सिर्फ ईमारत से कुछ दुरी पर खड़ा हो जाना है।

उसके बाद ईमारत के सबसे ऊपरी शिखर को नीचे से किसी लेजर लाइट की मदद से देखना है। अब नीचे से ईमारत के शिखर पर एक कोण बनेगा यह कोण उन्नयन कोण भी कहलाता है।

उसके बात ईमारत से कितनी दुरी पर आप खड़े हैं उसको भी नोट कीजिये। इससे इस समकोण त्रिभुज बनता है। जिसका एक कोण 90 डिग्री होगा और दूसरा कोण भी पता हो गया और आधार भी पता हो गया है। इन दोनों की मदद से आप ईमारत की ऊंचाई निकाल सकते हैं। चलिए शुरुआत से कुछ बेसिक चीजों के बारे में जान लेते हैं।

त्रिकोणमिति का मतलब

Trigonometry तीन ग्रीक शब्दों से मिल कर बना हुआ है। Tri का अर्थ तीन होता है। gon का अर्थ भुजा और metron का अर्थ माप। मतलब त्रिकोणमिति में तीन भुजाओं का माप होता है। त्रिकोणमिति में त्रिभुज के भुजा ,कोण के अनुपात का अध्ययन किया जाता है।

त्रिकोणमिति का उपयोग

प्राचीन समय में त्रिकोणमिति का उपयोग कर के तारों और ग्रहों के बीच की दुरी का पता लगाया जाता था। प्राचीन समय में त्रिकोणमिति पर किये गए कार्य का उल्लेख मिश्र और बेबीलोन में मिलता है।

त्रिकोणमितीय अनुपात

अनुपात क्या होता है ? इसके बारे में मैंने पहले ही डिटेल से बता दिया है। आप सबसे पहले इसके बारे में जान लीजिये उसके बाद त्रिकोणमितीय अनुपात के बारे में जानिएगा।

त्रिकोणमितीय अनुपात में हम समकोण त्रिभुज के भुजा के अनुपात और कोणों के अनुपात के बारे में पढ़ेंगे। त्रिकोणमितीय अनुपात में कुछ शब्द का उपयोग किया जाता है। चलिए सबसे पहले इन शब्दों के बारे में संक्षिप्त में जानते हैं।

sine :- Sine शब्द का प्रयोग 500 ई में आर्यभट्ट द्वारा लिखित पुस्तक आर्यभटियम में मिलता है। आर्यभट्ट ने शब्द अर्ध-ज्या का प्रयोग अर्ध-जीवा के लिए किया था जिसने समय-अंतराल में ज्या या जीवा का संक्षिप्त रूप ले लिया। इस आर्यभटियम पुस्तक को अरबी में अनुवाद किया गया, तब तब शब्द जीवा का यथावत रख लिया गया। शब्द जीवा को साइनस (Sinus) के रूप में अनुदित किया गया, जिसका अर्थ वक्र है। खगोलविद के एक अंग्रेजी प्रोफेसर एडमंड गुंटर ने पहले-पहल संक्षिप्त संकेत ‘sin’ का प्रयोग किया था।

cosine :- Cosine शब्द का उदय बहुत बाद में हुआ। cosine फलन का उदगम पूरक कोण के sine का अभिकलन करने को ध्यान में रखकर किया गया था। आर्यभट्ट ने इसे कोटिज्या का नाम दिया था। 1674 में अंग्रेजी गणितज्ञ सर जोनास मुरे ने पहले-पहल संक्षिप्त संकेत ‘cos’ का प्रयोग किया था।

Sin, Cos के उदगम के बाद tan, cot, sec, cosec का उदगम इन्हीं दोनों से हुआ। Sin, Cos, tan, cot, sec और cosec का कुछ मतलब नहीं होता है जबतक कि उसके कोण जुड़ा ना हो जैसे Sin A , Cos A, tan A , cot A , sec A और cosec A का मतलब होता है। यहां A का मतलब कोण होता है। कोण को डिग्री में लिखा जाता है। कोण के बारे में मैंने डिटेल से पोस्ट लिखा है पहले उसके बारे में पढ़ लीजिये। Sin A का मतलब Sin और A का गुणा नहीं होता है।

• आकृतियों, कोणों, रेखाओं की समझ और परिभाषा (Shapes, Angles, Lines )

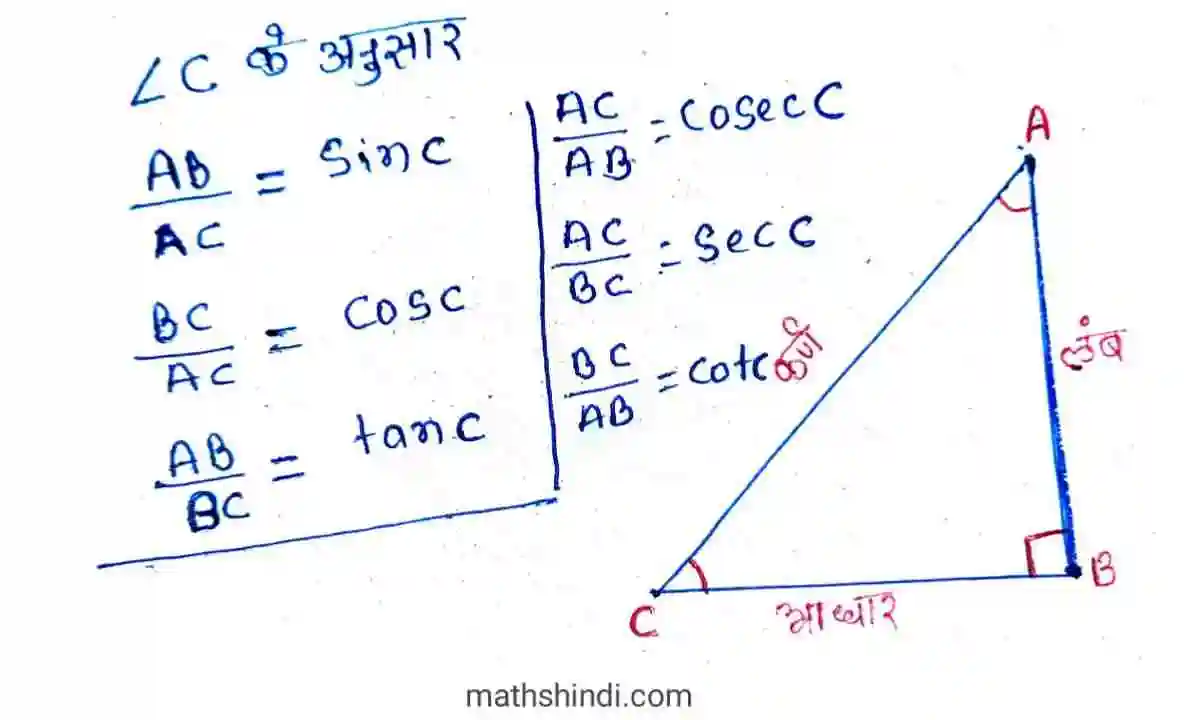
माना एक समकोण त्रिभुज ABC में कोण B समकोण है। कोण A और कोण C न्यूनकोण है। और भुजा AC = कर्ण, भुजा AB = लम्ब , भुजा BC = आधार है। तो,Sin, Cos के उदगम के बाद tan, cot, sec, cosec

1. AB/AC = sin C = लम्ब/कर्ण
2. BC/AC = cos C = आधार/कर्ण
3. AB/BC = tan C = लम्ब /आधार
4. AC/AB = cot C = आधार /लम्ब
5. AC/BC = sec C = कर्ण/आधार
6. BC /AB = cosec C = कर्ण/लम्ब

कोणों के त्रिकोणमितीय अनुपात

त्रिकोणमिति के कोणों के अनुपात में सभी कोणों का मान निकलना नहीं है। कुछ विशिष्ट कोणों का मान ही ज्ञात किया जाता है। जैसे 0°, 30°, 45°, 60° और 90°.

जैसे ,Sin 0° ,Cos45° इत्यादि का मान कितना होता है ? इसके बारे में मैंने नीचे टेबल में बता दिया है। लेकिन आप एक अच्छे छात्र हैं तो आप जरूर सोचते होंगे कि इसका मान कैसे निकाला जाता है ? अगर आप जानना चाहते हैं तो आप टेलीग्राम पर जुड़ सकते हैं। मैं यहाँ नहीं बताऊंगा क्योंकि यहाँ बोरिग हो जाएगा।

कोण A	0°	30°	45°	60°	90°
sin A	0	1/2	1/√2	√3/2	1
cos A	1	√3/2	1/√2	1/2	0
tan A	0	1/√3	1	√3	अपरिभाषित
cosec A	अपरिभाषित	2	√2	2/√3	1
sec A	1	2/√3	√2	2	अपरिभाषित
cot A	अपरिभाषित	√3	1	1/√3	0

पूरक कोणों के त्रिकोणमितीय अनुपात

जब दो कोणों का योग 90° के बराबर होता है तो उसे पूरक कोण कहा जाता है। नीचे कुछ सूत्र दिया गया है इसे याद रखना बहुत जरुरी है। यह याद रखने में दिक्कत नहीं होगी।

यह सूत्र कैसे बना इसके बारे में डिटेल से नहीं बताया गया है। अगर आप इसे डिटेल में जानना चाहते हैं तो आप मुझे प्रिवेट मेसेज कर सकते हैं। आपको वीडियो या पीडीऍफ़ उपलब्ध करा दिया जायेगा।

sin (90°-A) = cos A

cos (90°-A) = sin A

tan (90°-A) = cot A

cot (90°-A) = tan A

sec (90°-A) = cosec A

cosec (90°-A) = sec A

त्रिकोणमितीय सर्वसमिकाएँ

यहाँ कुछ सर्वसमिकाएँ दी गई है और इसका एक्सप्लनेशन भी नीचे दिया गया है। चलिए देखते हैं सबसे पहले सर्वसमिका के बारे में।

इन सभी सर्वसमिकाओं को प्रूफ करने के लिए एक समकोण त्रिभुज ABC लेते हैं। जिसमें कोण B समकोण है। कोण A और C न्यूनकोण है। इस त्रिभुज में कोण A के अनुसार भुजा AC कर्ण है। भुजा BC आधार है और भुजा AB लम्ब है।

त्रिभुज ABC में त्रिकोणीय अनुपात के अनुसार,

sin A = BC/AC, cos A = AB/AC, tan A = BC/AB, cot A = AB/BC, sec A = AC/AB, cosec A = AC/BC,

cos²A + sin²A =1

त्रिभुज ABC में ,जहाँ कोण B समकोण है। इसलिए इसे हम लिख सकते हैं, AB² + BC² = AC² ………….(1) (1) के प्रत्येक पद को AC² से भाग देने पर हमें प्राप्त होता है। AB²/AC² + BC²/AC² = AC²/AC² or, (AB/AC )² + (BC/AC )² = (AC/AC )² or, (cos A )² + (sin A )² = 1 or, cos² A + sin² A = 1

1 + tan²A = sec²A , यहाँ कोण A = 90 डिग्री नहीं है।

त्रिभुज ABC में ,जहाँ कोण B समकोण है। इसलिए इसे हम लिख सकते हैं, AB² + BC² = AC² ………….(1) (1) के प्रत्येक पद को AB² से भाग देने पर हमें प्राप्त होता है। AB²/AB² + BC²/AB² = AC²/AB² or, (AB/AB )² + (BC/AB )² = (AC/AB)² or, 1 + (tan A )² = (sec A )² or, 1 + tan² A = sec² A

cot²A + 1 = cosec²A , यहाँ कोण A = 0 डिग्री नहीं है ।

त्रिभुज ABC में ,जहाँ कोण B समकोण है। इसलिए इसे हम लिख सकते हैं, AB² + BC² = AC² ………….(1) (1) के प्रत्येक पद को BC² से भाग देने पर हमें प्राप्त होता है। AB²/BC² + BC²/BC² = AC²/BC² or, (AB/BC )² + (BC/BC)² = (AC/BC)² or, (cot A )² + 1 = (cosec A )² or, cot²A + 1 = cosec²A

सारांश और सूत्र

• sin C = लम्ब/कर्ण
• cos C = आधार/कर्ण
• tan C = लम्ब /आधार
• cot C = आधार /लम्ब
• sec C = कर्ण/आधार
• cosec C = कर्ण/लम्ब
• sin 0° = 0
• sin 30° = 1/2
• sin 45° = 1/√2
• sin 60° = √3/2
• sin 90° = 1
• cos 0° = 1
• cos 30° = √3/2
• cos 45° = 1/√2
• cos 60° = 1/2
• cos 90° = 0
• tan 0° = 0
• tan 30° = 1/√3
• tan 45° = 1
• tan 60° = √3
• tan 90° = अपरिभाषित
• cot 0° = अपरिभाषित
• cot 30° = √3
• cot 45° = 1
• cot 60° = 1/√3
• cot 90° = 0
• sec 0° = 1
• sec 30° = 2/√3
• sec 45° = √2
• sec 60° = 2
• sec 90° = अपरिभाषित
• cosec 0° = अपरिभाषित
• cosec 30° = 2
• cosec 45° = √2
• cosec 60° = 2/√3
• cosec 90° = 1
• sin (90°-A) = cos A
• cos (90°-A) = sin A
• tan (90°-A) = cot A
• cot (90°-A) = tan A
• sec (90°-A) = cosec A
• cosec (90°-A) = sec A
• cos²A + sin²A =1
• cos²A = 1 – sin²A
• sin²A = 1 – cos²A
• 1 + tan²A = sec²A
• tan²A = sec²A – 1
• cot²A + 1 = cosec²A
• cosec²A – cot²A = 1
• sin A = 1/cosec A
• cos A = 1/sec A
• tan A = 1/cot A
• cot A = 1/tan A
• sec A = 1/cos A
• cosec A = 1/sin A

आप मुझे YouTube , Telegram पर भी फ्लो कर लीजिए।

Class 10 Maths Topic (थ्योरी )

1. Chapter 1: वास्तविक संख्या (Real Numbers)
2. Chapter 2: बहुपद (Polynomials)
3. Chapter 3: दो चर वाले रैखिक युग्म (Pair of Linear Equations in Two Variables)
4. Chapter 4: द्विघात समीकरण (Quadratic Equations)
5. Chapter 5: समांतर श्रेढ़ियाँ (Arithmetic Progressions)
6. Chapter 6: त्रिभुज (Triangles)
7. Chapter 7: निर्देशांक ज्यामिति (Coordinate Geometry)
8. Chapter 8: त्रिकोणमिति का परिचय (Introduction to Trigonometry)
9. Chapter 9: त्रिकोणमिति के कुछ अनुप्रयोग (Some Applications of Trigonometry)
10. Chapter 10: वृत (Circles)
11. Chapter 11: रचनाएँ (Constructions)
12. Chapter 12: वृतों से संबंधित क्षेत्रफल (Areas Related to Circles)
13. Chapter 13: पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes)
14. Chapter 14: सांख्यकी (Statistics)
15. Chapter 15: प्रायिकता (Probability)

व्यापार नॉलेज :-

1.शेयर मार्केट क्या होता है (Stock Market)

2.ट्रेडिंग कैसे करें और क्या होता है (Trading)

3. म्यूच्यूअल फंड क्या होता है (Mutual Fund)