वृत (Circles) क्लास -10 NCERT गणित चैप्टर नंबर 10

क्लास 10 के NCERT गणित का यह 10वां चैप्टर है। इस चैप्टर में वृत (circle) के बारे में पढ़ेंगे। वृत के बारे में हरेक जानकारी दी जाएगी। मेरे द्वारा लिखें इस पोस्ट को पढ़ने से आप वृत को बहुत हल्का टॉपिक समझेंगे। सबसे पहले वृत के बारे में जानेंगे।

वृत क्या होता है ?

वृत एक ऐसा बंद आकृति है जो एक कर्व रेखा से बनी होती है। और केंद्र से हरेक दशा में कर्व रेखा की दूरी एक समान होती है। 

वृत की त्रिज्या (Radius)

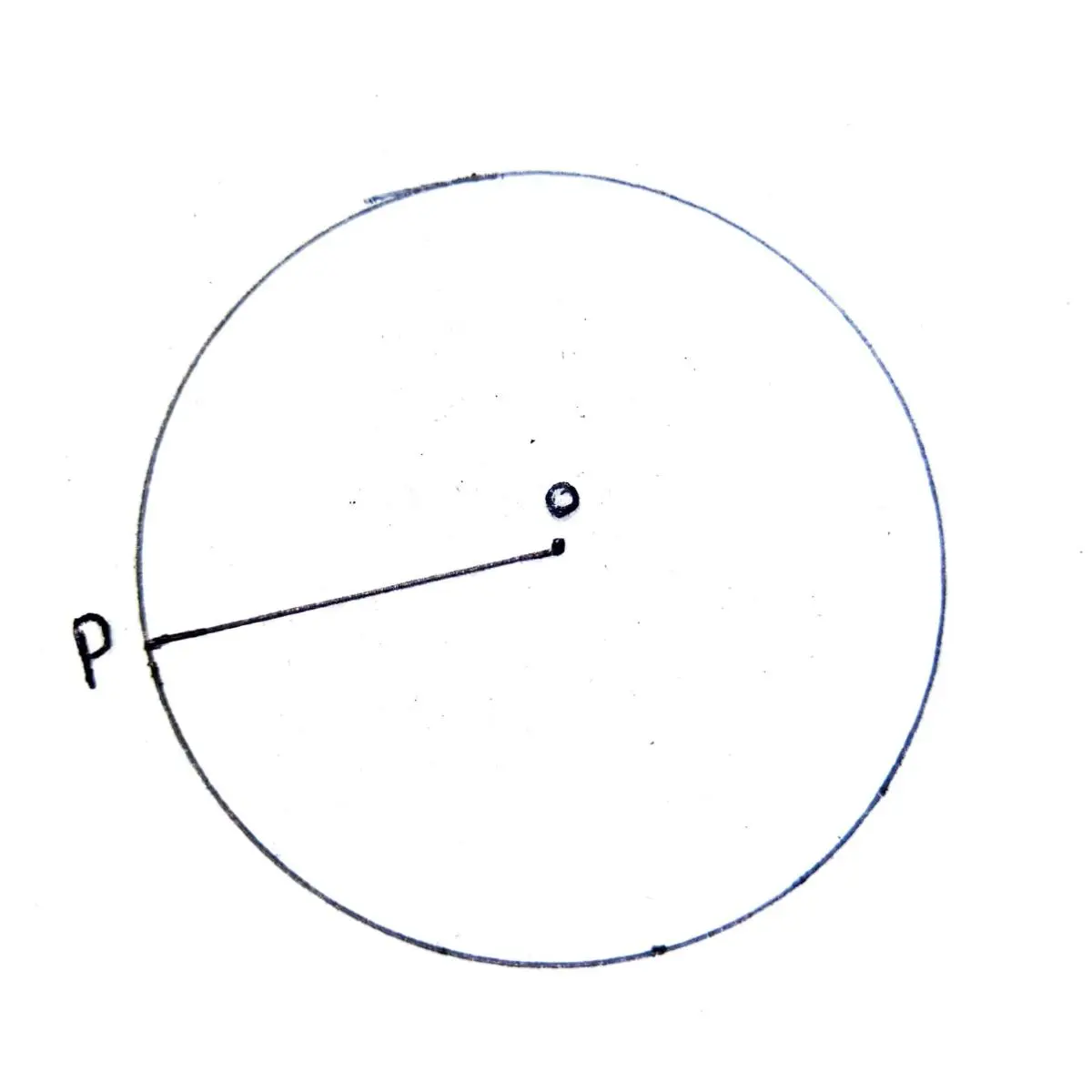
वृत के केंद्र से कर्व रेखा की दूरी को त्रिज्या कहा जाता है। केंद्र से कर्व रेखा पर एक से अधिक त्रिज्या रेखा खिंची जा सकती है। लेकिन सभी त्रिज्या रेखा की दूरी एक समान होती है। त्रिज्या को शार्ट में r लिखा जाता है। क्योंकि यहाँ “R” का मतलब होगा Radius होगा।

ऊपर के चित्र में OP वृत का त्रिज्या है। वृत का केंद्र बिंदु O है।

वृत की जीवा

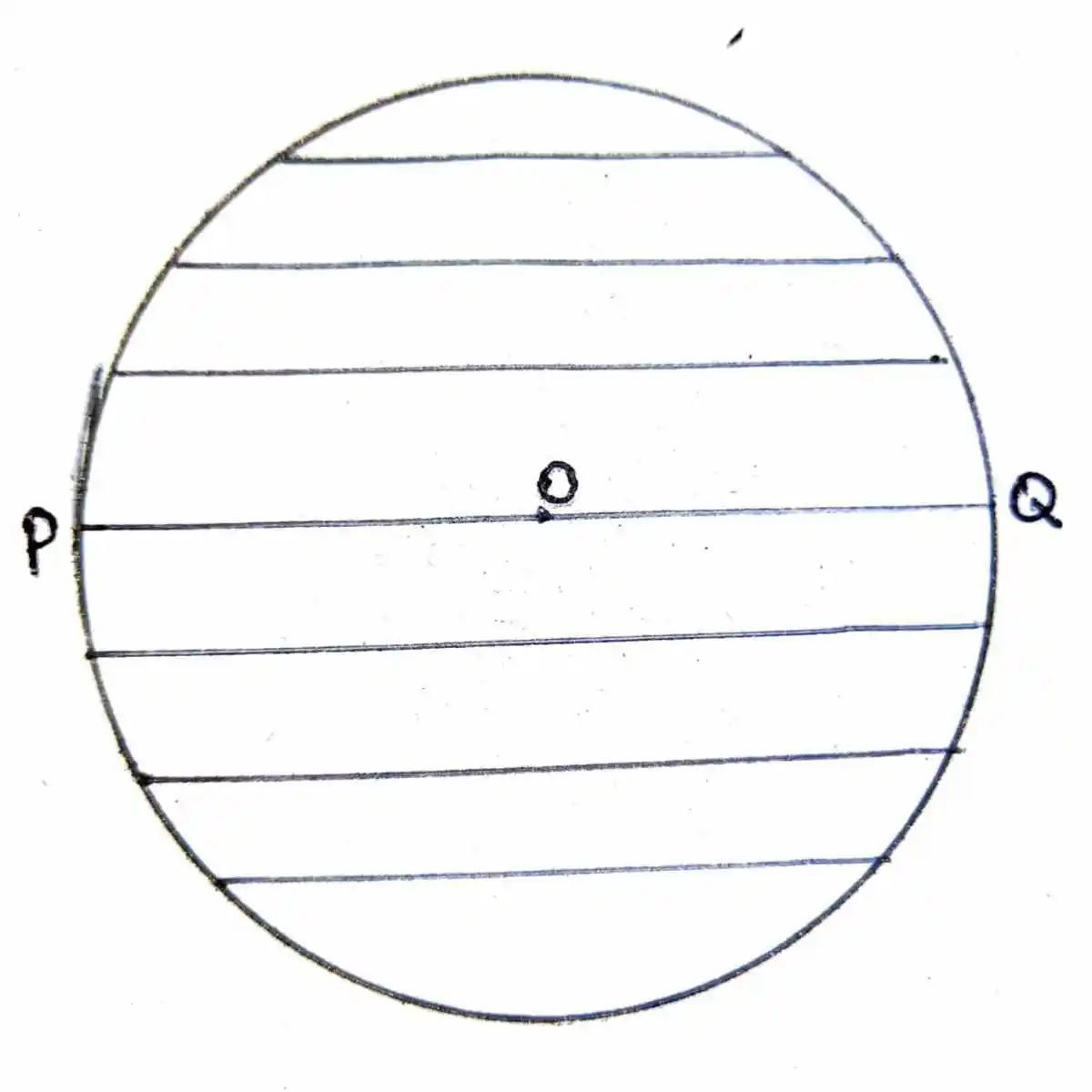
वृत के कर्व रेखा (परिधि) को प्रतिच्छेद करने वाली रेखा जीवा कहलाती है। वृत पर अनन्त जीवा खिंची जा सकती है। सबसे लंबी जीवा केंद्र से होकर गुजरती है। नीचे के चित्र में सबसे बड़ी जीव POQ है, जो केंद्र बिंदु O से गुजरती है। आप नीचे वृत पर देख सकते हैं केंद्र से दूर जाने पर जीव की लम्बाईयाँ कम होती जा रही है।

वृत की व्यास (Diameter)

वृत की व्यास रेखा जीवा रेखा ही है। सबसे बड़ी जीवा जो वृत के केंद्र से होकर गुजरती है उसे व्यास कहा जाता है। व्यास को शार्ट में D लिखा जाता है। यहाँ “D” का मतलब होता है Diameter. ऊपर के चित्र में देख सकते हैं। POQ व्यास है। एक वृत पर सिर्फ एक व्यास खिंचा जा सकता है।

दो त्रिज्या (r) को जोड़ देंगे तो एक व्यास (D) होता है। मतलब व्यास = 2× त्रिज्या . D = 2r

π क्या होता है ?

π एक यूनानी अक्षर है , इसे पाई पढ़ा जाता है। भारतीय गणितज्ञ आर्यभट्ट (476-550 ई.पू.) ने π का निकटतम मान दिया था। उन्होंने कहा कि π = 62832/20000 होता है, जो लगभग 3.1416 के बराबर है।

π एक अपरिमेय (irrational) संख्या है और इसका दशमलव प्रसार अनवसानी और अनावर्ती (non-terminating and non-repeating) होता है। परंतु व्यवहारिक कार्यों के लिए π का मान 22/7 या 3.14 लेते हैं।

वृत की परिधि (Circumference)

वृत की कर्व रेखा की लंबाई को परिधि कहा जाता है। अगर त्रिज्या या व्यास दिया रहता है तो उसकी मदद से वृत की परिधि निकाला जा सकता है। परिधि (Circumference) = 2πr या, परिधि = Dπ [ यहाँ, D=2r, π (पाई) = पाई (π) का मान कांस्टेंट होता है इसका मान 3.1415 होता है या इसको लगभग में 22/7 भी लिखा जाता है।

वृत की चाप

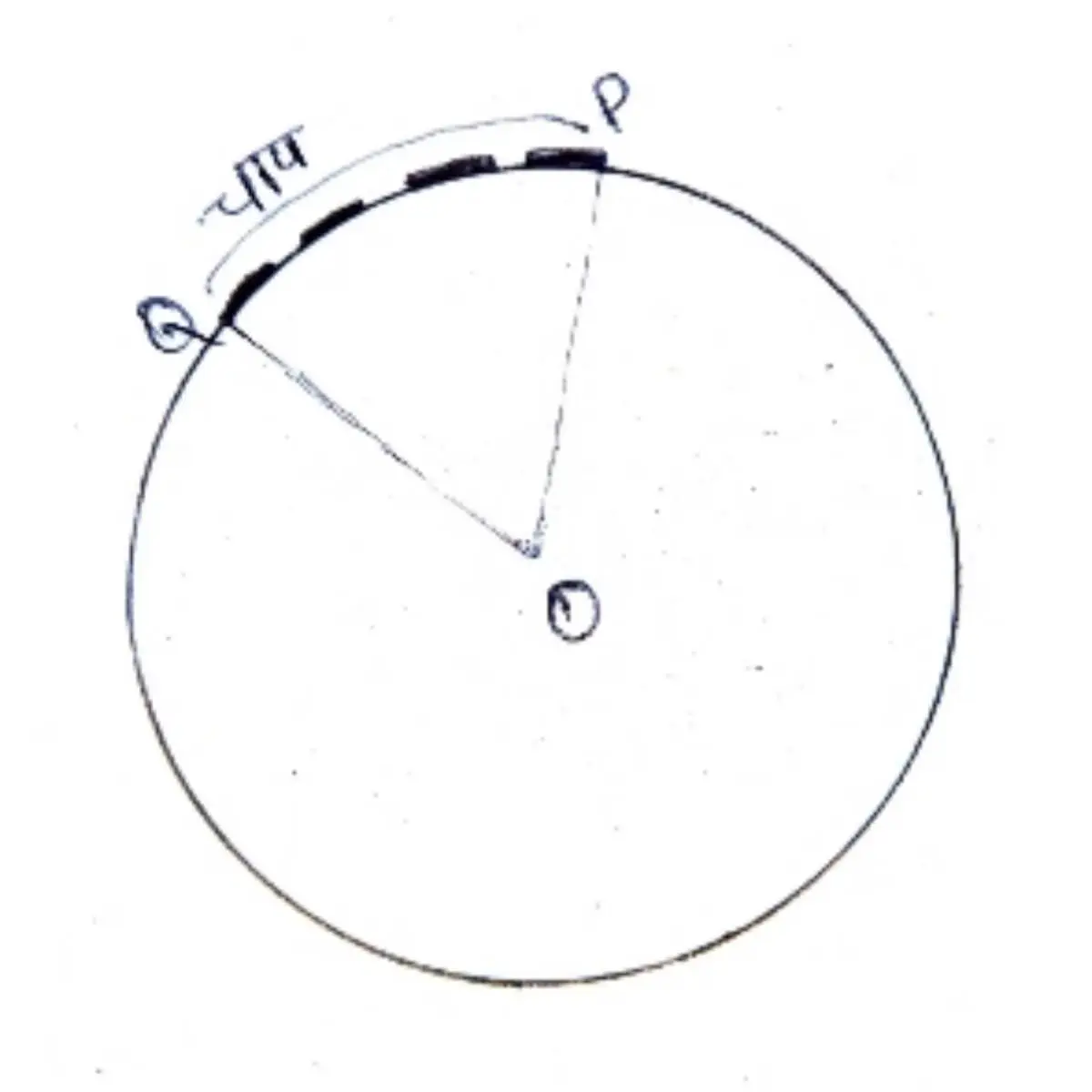
इस चित्र में देख सकते हैं। PQ एक कर्व रेखा है। इस रेखा को खींचने के लिए वृत के केंद्र से चाप की मदद से PQ कर्व रेखा खिंची गई है। इस चाप को अगर पूरा घुमा देगें तो वृत बन जायेगा। PQ को लघु चाप कहा जायेगा। और Q से लंबी दूरी तय कर P पर जाने से जो चाप खंड होगा वह दीर्घ चाप (QP) कहलायेगा।

वृत का क्षेत्रफल (Area)

क्षेत्रफल क्या होता है इसके बारे में मैंने पहले बेसिक गणित में बता दिया है। सभी बंद आकृतियों का क्षेत्रफल निकाला जाता है। वृत के क्षेत्रफल का भी सूत्र होता है। वृत का क्षेत्रफल (Circle of Area) = πr²

वृत का वृतखंड (segment of a circle)

वृत का वह क्षेत्र जो एक जीवा और संगत चाप से घिरा होता है, वह क्षेत्र वृतखंड कहलाता है।

इस आकृति में देख सकते हैं। छोटे वाले खंड को लघु वृतखण्ड और बड़े वाले को खंड को दीर्घ वृतखंड कहलायेगा। अगर व्यास और संगत चाप से घिरा वृतखंड हो तो उसे अर्द्ध-वृत कहा जायेगा।

वृतखंड का परिमाप :- वृतखंड का परिमाप निकलने के लिए, संगत जीव और चाप की लंबाई जो जोड़ दिया जाता है।

वृतखंड का क्षेत्रफल :- पूरा वृत का क्षेत्रफल निकाल कर दीर्घ वृतखंड का क्षेत्रफल घटाने पर लघुवृतखण्ड का क्षेत्रफल निकल जाता है। वहीं लघुवृतखण्ड का क्षेत्रफल घटाने से दीर्घ वृतखंड का क्षेत्रफल निकल जाता है।

वृत का त्रिज्याखंड (sector of a circle)

वृत का वह क्षेत्र जो दो त्रिज्याओं और संगत चाप से घिरा होता है, वह क्षेत्र त्रिज्याखंड कहलाता है।

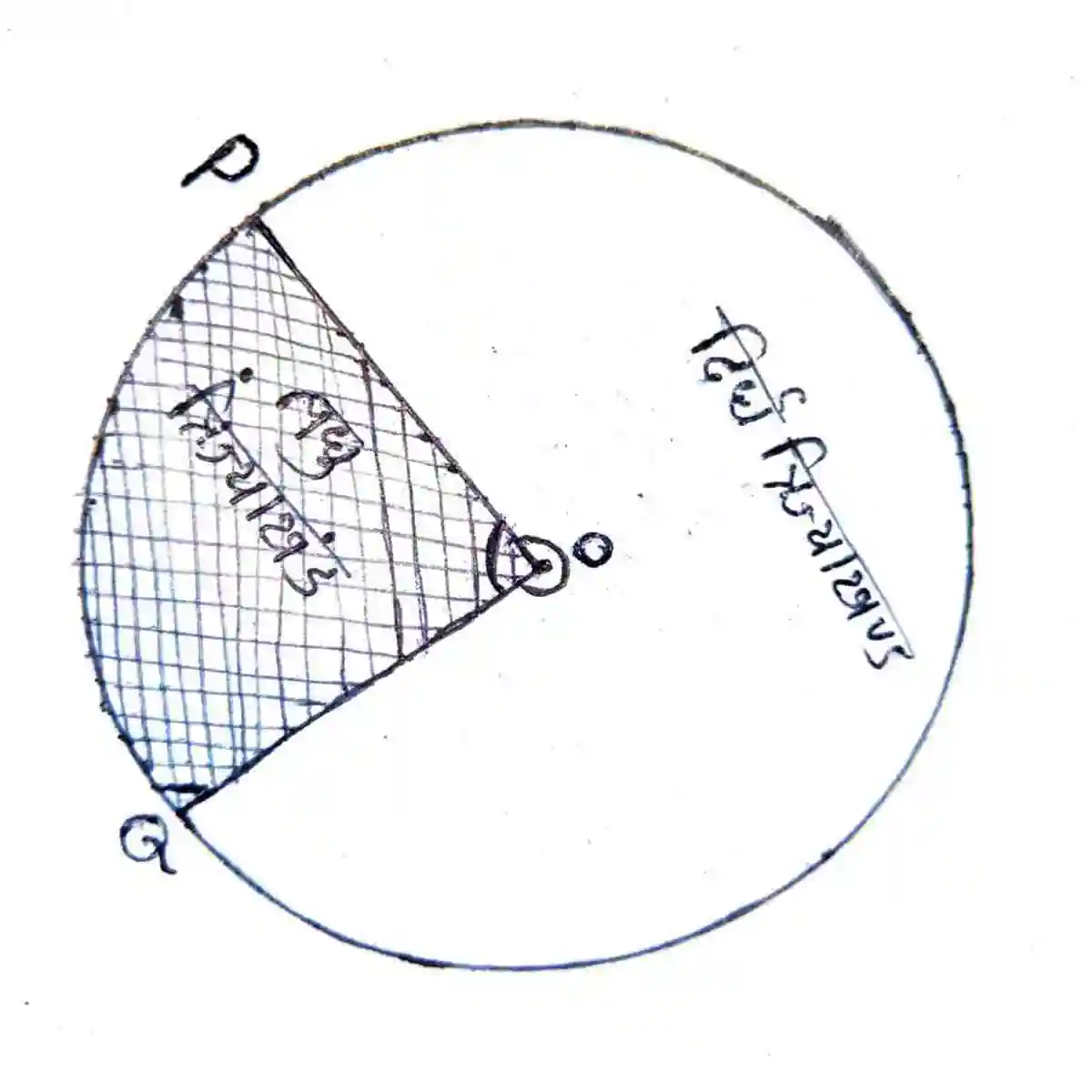
किस आकृति में देख सकते हैं। एक लघु त्रिज्यखंड है और दूसरा दृर्घ त्रिज्याखंड है। इस आकृति में दो त्रिज्याएँ OP और OQ संगत चाप PQ से जुड़ा है , इस वृत में POQ वाले क्षेत्र को लघु त्रिज्याखंड कहा जाता है। प्रश्न में अक्सर त्रिज्याखंड का क्षेत्रफल निकलने के लिए कहा जाता है। कभी-कभी परिमाप भी निकलने के लिए कहा जाता है। यह बहुत आसान है।

त्रिज्याखंड का परिमाप :- त्रिज्याखंड का परिमाप निकलने के लिए दो त्रिज्याएँ और संगत चाप को जोड़ा जाता है। चाप की लंबाई निकलने के लिए , वृत की परिधि में त्रिज्याखंड के कोण से गुणा किया जाता है और 360° से भाग दिया जाता है। जैसे त्रिज्याखंड के कोण 60° है तो त्रिज्याखंड का परिमाप = (2πr×60°)/360° +2r

त्रिज्याखंड का क्षेत्रफल :- वृत के त्रिज्याखंड का क्षेत्रफल निकालना भी बहुत आसान है। प्रश्न में खासकर त्रिज्याखंड के क्षेत्रफल निकालने के लिए कहा जाता है। इसका फॉर्मूला होता है। खैर बिना फार्मूला का भी निकाल सकते हैं। अगर त्रिज्याखंड का कोण का माप ∅ है तो त्रिज्याखंड का क्षेत्रफल = πr²∅/360° होगा।

वृतखंड और त्रिज्याखंड में लघुखण्ड और दृर्घ खंड निकलता है। सवाल में अगर वृतखंड या त्रिज्याखंड आता है तो उसे लघुखण्ड ही माना जाता है।

वृत और एक रेखाओं की स्थिति

वृत पर रेखाओं की सिर्फ तीन ही स्थितियां होती है। अप्रतिछेदी रेखा, प्रतिछेदी (छेदक) रेखा और स्पर्श रेखा।

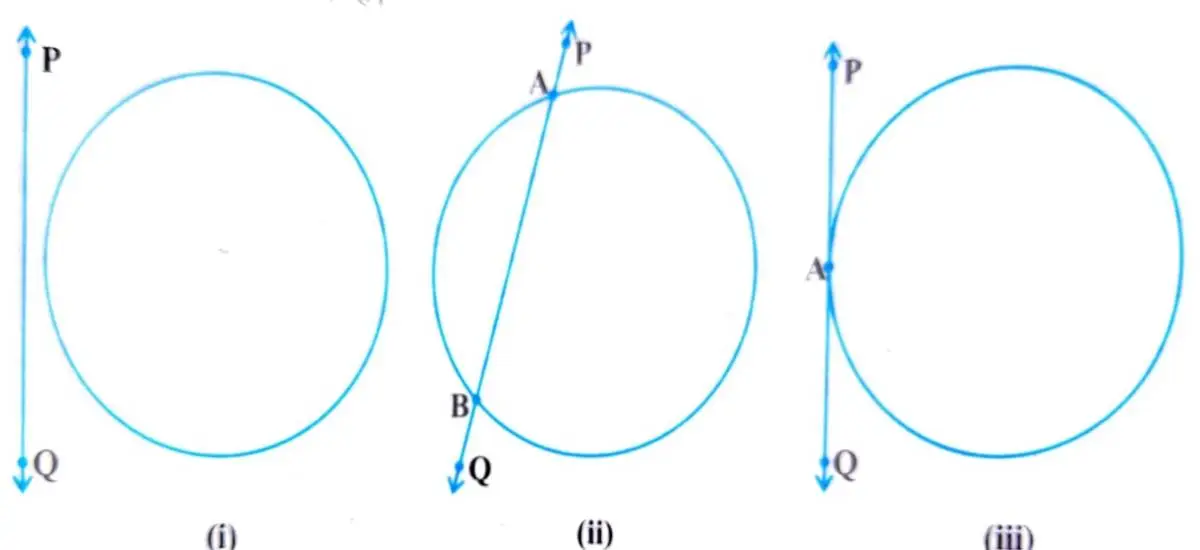
वृत पर अप्रतिछेदी रेखा

वैसी रेखा जो वृत के बाहर होती है और वृत्त को छूकर नहीं गुजरती है उसे अप्रतिछेदी रेखा कहा जाता है। ऊपर के चित्र संख्या (i) में दिखाए गए वृत और रेखाओं की स्थिति देख सकते हैं। अगर वृत के बाहर कोई बिंदु हो और वृत के कर्व रेखा को छू कर न गुजरे तब ऐसी रेखा अप्रतिछेदी रेखा कहलायेगा।

वृत पर छेदक रेखा

वाइसी रेखा जो वृत को दो बिन्दुओं पर प्रतिच्छेद करके निकलती है उसे छेदक रेखा या प्रतिछेदी रेखा कहा जाता है। ऊपर के चित्र संख्या (ii) को देख सकते हैं। दो बिंदु A और B वृत के कर्व रेखा पर है इससे बने रेखा छेदक रेखा या प्रतिछेदी रेखा कहलाता है।

वृत की स्पर्श रेखा

वैसे ही रेखा जो वृत्त के ऊपर किसी एक बिंदु से छुकरके गुजरती है उसे स्पर्श रेखा कहा जाता है। ऐसा चित्र संख्या (iii) में देख सकते हैं। क्या इस रेखा को प्रतिछेदी रेखा कहेंगे ? नहीं, ऐसी रेखा प्रतिछेदी रेखा नहीं कहलाती है। जो रेखा वृत को कम से कम दो बिंदु पर प्रतिच्छेद करेगी तब वह प्रतिछेदी रेखा कहलाती है।

किसी वृत की स्पर्श रेखा वह रेखा है जो वृत को केवल एक बिंदु पर प्रतिच्छेद करती है।

• वृत के एक बिंदु पर एक और केवल एक स्पर्श रेखा होती है।
• किसी वृत की स्पर्श रेखा छेदक रेखा की एक विशिष्ट दशा है जब संगत जीवा के दोनों सिरे सम्पती हो जाएं।

अच्छी जानकारी :- (जरूर पढ़ें)

• ट्रेडिंग क्या होता है ?
• शेयर मार्केट क्या होता है ?

वृत की स्पर्श बिंदु

• वृत के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लम्ब होती है ।

• एक वृत की कितनी स्पर्श रेखाएँ हो सकती हैं ? एक वृत पर अनंत स्पर्श रेखाएँ हो सकती है। किसी बाह्य बिंदु से वृत पर सिर्फ दो स्पर्श रेखा डाला जा सकता है। वहीं वृत के अंतः बिंदु से से वृत के ऊपर कोई स्पर्श रेखा नहीं खिंचा जा सकता है। वृत के परिधि पर स्थित बिंदु से वृत पर सिर्फ एक स्पर्श रेखा खिंचा जा सकता है।

• किसी वृत्त की स्पर्श रेखा उसे कितने बिंदुओं पर प्रतिच्छेद करते हैं ? सिर्फ एक बिंदु पर ही प्रतिच्छेद करती है।

• वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को क्या कहते हैं? छेदक रेखा कहा जाता है।

• एक वृत्त की कितनी समांतर स्पर्श रेखाएं हो सकती है? सिर्फ दो समांतर स्पर्श रेखा हो सकती है।

• वृत तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को क्या कहते हैं ? स्पर्श बिंदु कहा जाता है।

एक बिंदु से एक वृत्त पर पर स्पर्श रेखाओं की संख्या

किसी वृत्त पर किसी बिंदु से खींची गई स्पर्श रेखाओं की संख्या के बारे में चलिए जानते हैं। सिर्फ तीन ही स्थिति होती है। वृत्त के बाह्य बिंदु से खिंची गई रेखा। वृत के अंतः बिंदु से खींची गई रेखा। और वृत के ऊपर (स्पर्श बिंदु से) खिंची गई रेखा।

1.वृत के अंदर बिंदु से वृत पर रेखा

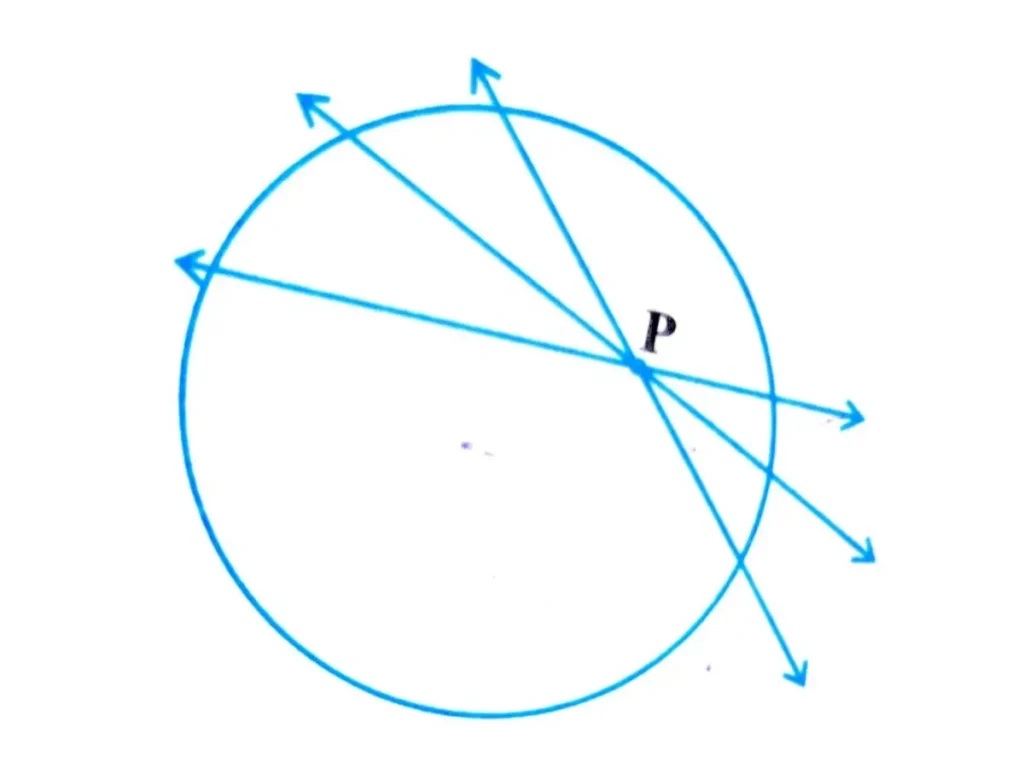
वृत्त के अंदर अगर कोई बिंदु है तो उससे वृत के ऊपर स्पर्श रेखा नहीं खींची जा सकती है। जो भी रेखा होगी वह छेदक रेखा का कहलाएगी।

2.वृत के ऊपर बिंदु से वृत पर रेखा

अगर वृत के ऊपर कोई स्पर्श बिंदु है तो उससे सिर्फ एक ही स्पर्श रेखा खींची जा सकती है।

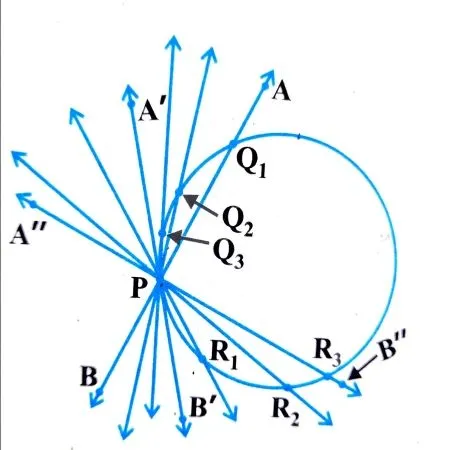
3.वृत के बाहर बिंदु से वृत पर रेखा

वृत के बाहर कोई बिंदु है तो उस बिंदु से वृत्त के ऊपर सिर्फ दो स्पर्श रेखा खींची जा सकती हैं।

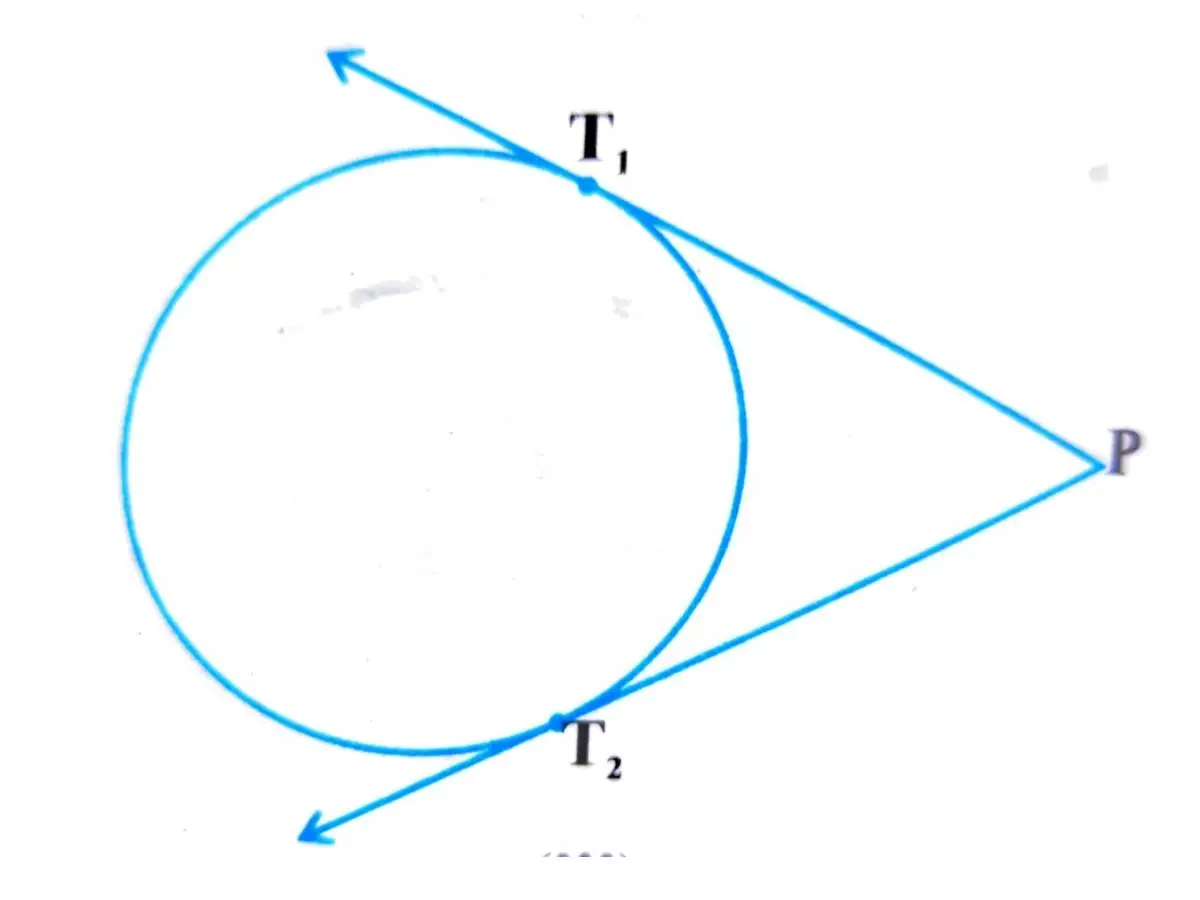
वाह्य बिंदु से वृत पर खींची गई स्पर्श रेखाओं की लम्बाईयाँ बराबर होती है।

यहाँ वृत के बाहर एक बिंदु P है। इस P बिंदु से इस वृत पर सिर्फ दो स्पर्श रेखा PT1 और PT2 ही खिंचा जा सकता है। इसके अलावा कोई स्पर्श रेखा नहीं खिंचा जा सकता है।

सूत्र :-

• त्रिज्या (r) = व्यास (D)/2
• व्यास (D) = 2× त्रिज्या (r)
• वृत की परिधि = 2πr
• वृत का क्षेत्रफल =πr²
• त्रिज्याखंड का क्षेत्रफल = (πr² × त्रिज्याखंड का कोण)/360°
• त्रिज्याखंड का परिमाप = (2πr×त्रिज्याखंड का कोण)/360° +2r

आप मुझे YouTube , Telegram पर भी फ्लो कर लीजिए।