त्रिकोणमिति के कुछ अनुप्रयोग क्लास 10 के गणित का चैप्टर नंबर 9 है। इससे पहले त्रिकोणमिति का परिचय पढ़ चुके हैं। अगर आप नहीं पढ़े हैं तो सबसे पहले आप पढ़ लीजिए उसके बाद इस चैप्टर को पढियेगा तब समझ में आएगा।
इस चैप्टर में त्रिकोणमिति के प्रयोग पर जुड़ा सवाल होगा। त्रिकोणमिति का उपयोग अभी के समय में ही नहीं बल्कि बहुत पहले भी क्या जाता था। खासकर खगोल विद इसका प्रयोग पृथ्वी से ग्रहों और तारों की दूरियां निकालने के लिए करते हैं। त्रिकोणमिति का प्रयोग भूगोल और नौचालन में भी किया जाता है।
त्रिकोणमिति का उपयोग करते हुए 1852 में सर्वेक्षण के दौरान विश्व के सबसे ऊंचे पर्वत की खोज की गई थी।
इस चैप्टर में हम यह देखेंगे कि किस प्रकार वास्तव में बिना माप किए बिना ही त्रिकोणमिति का प्रयोग विभिन्न वस्तुओं की ऊँचाइयाँ को दूरियाँ ज्ञात करने में किया जाता है।
Table of Contents
ऊँचाइयाँ और दूरियां (Height & Distance)
ऊंचाइ और दूरी की मदद से इस चैप्टर में बड़े से बड़े टावर, बिल्डिंग इत्यादि । चीजों का माप निकाला जाएगा वो भी त्रिकोणमितीय फार्मूला का उपयोग करके। कुछ ऐसे शब्द आएंगे जिसका मतलब पता होना चाहिए। जैसे :- दृष्टि रेखा, क्षैतिज रेखा,ऊर्ध्वाधर रेखा, उन्नयन कोण और अवनमन कोण । नीचे सभी का परिभाषा लिखा गया है। पहले इसको अच्छी तरह समझ लीजिए।
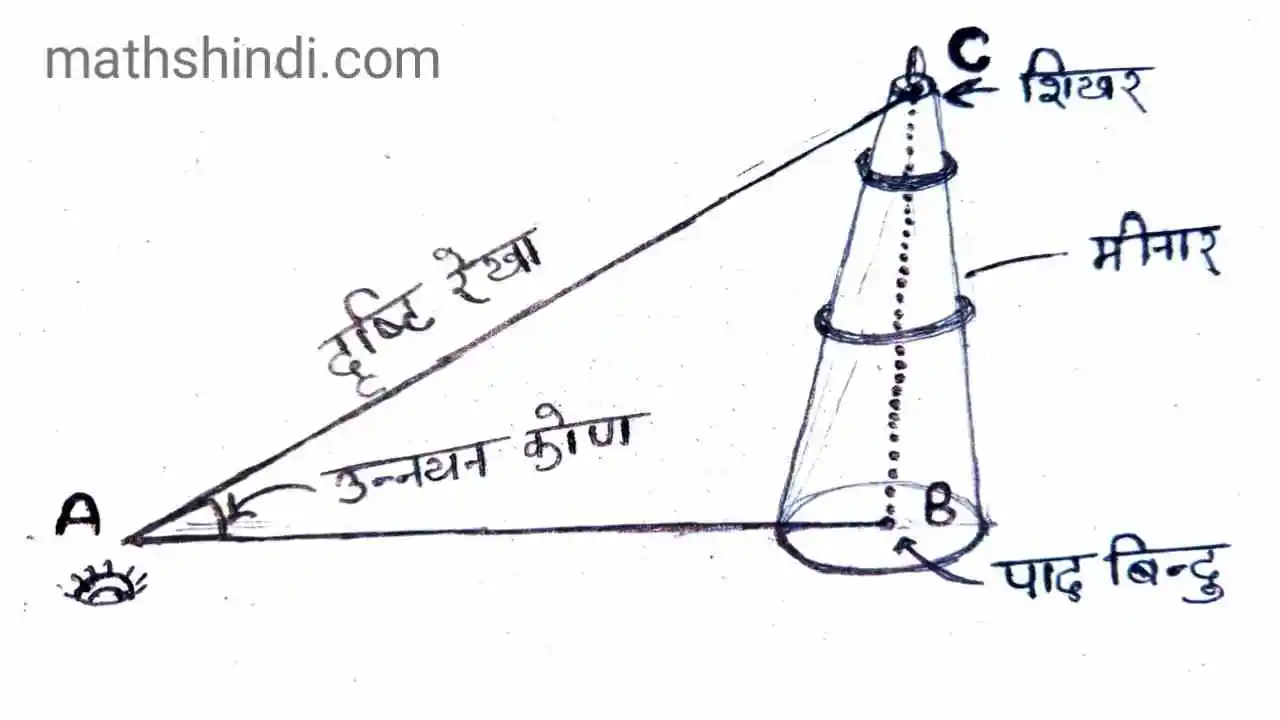
दृष्टि रेखा (Line of sight)
इस आकृति में AC रेखा को दृष्टि रेखा कहा जाएगा क्योंकि एक इंसान बिंदु A बिंदु C की तरफ देख रहा है। आँखों से देंखने पर जो रेखा बनती है उसे दृष्टि रेखा कहा जाता है। इस आकृति में AC रेखा दृष्टि रेखा है।
क्षैतिज रेखा (Horizontal Line)
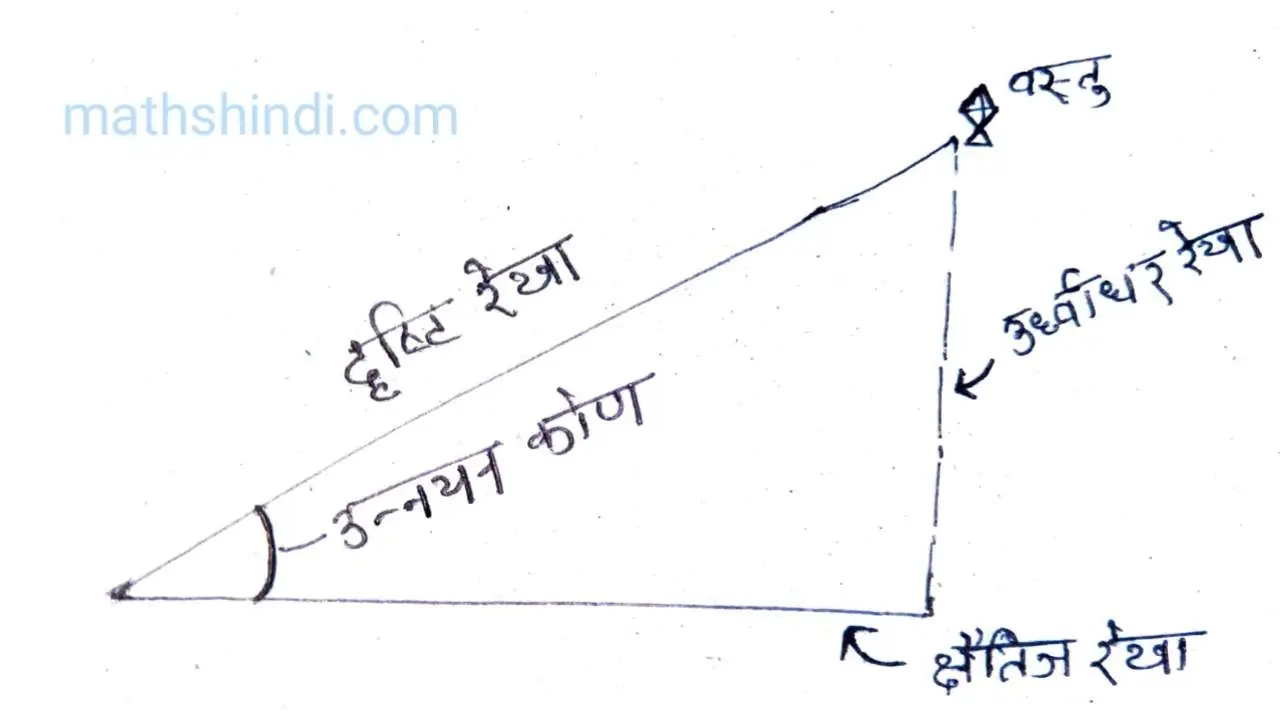
क्षैतिज रेखा, वह रेखा होती है जो धरती पर सीधी खींची जाती है, या धरती के समानांतर खींची जाती है। वैसे बहुत लोग भूल करते है अगर रेखा तिरछी होती है तो उसे क्षैतिज कह दिया जाता है लेकिन यह गलत है। क्षैतिज रेखा हमेशा धरती के समानांतर होती है।
ऊर्ध्वाधर रेखा (Vertical Line)
ऊर्ध्वाधर रेखा उस रेखा को कहते हैं जो धरती से लंबवत खड़ी रहती है। वैसे जो खड़ी लाइन होती है उसे vertical line या ऊर्ध्वाधर रेखा कहा जाता है। ऊर्ध्वाधर रेखा हमेशा धरती पर सीधी खड़ी रहती है।
उन्नयन कोण (Angle of elevation)
इस आकृति में दृष्टि रेखा और क्षैतिज रेखा से मिलकर जो कोण बन रहा है वह उन्नयन कोण है। इस कोण का उपयोग इस चैप्टर में हमेशा होगा।
अवनमन कोण (Angle of depression)
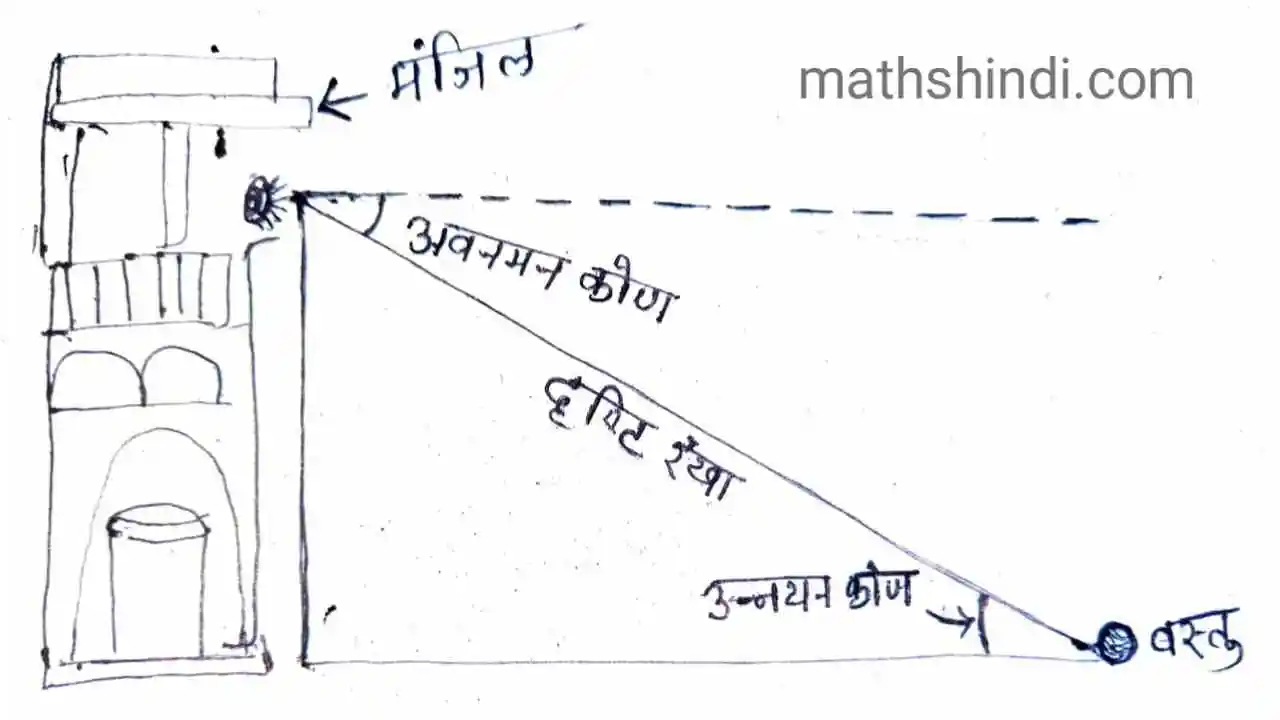
अवनमन कौन भी क्षैतिज रेखा और दृष्टि रेखा से बने होते हैं। अवनमन कोण तब बनता है, जब इंसान ऊपर ( किसी टावर, मंजिल इत्यादि) से नीचे रखे वस्तु को देखता है। इस चित्र में देख सकते हैं आंखों से सीधी और धरती के समानांतर रेखा (AB) भी क्षैतिज रेखा है। ऊपर से नीचे रखें वस्तु को देखता है तो यह रेखा (BC) दृष्टि रेखा है। इसलिए कोण CBA को अवनमन कोण कहेंगे।
सवाल में अगर अब नमन कौन आए तो उसे चित्र बनाकर पहले समझ ले, उसके बाद उन्नयन कोण निकाले, उसके बाद सवाल को हल करने की कोशिश करें।
Q1. भूमि के एक बिंदु से जो मीनार के पाद बिंदु से 30 मीटर की दूरी पर है मीनार के शिखर का उन्नयन कोण 30 डिग्री है मीनार की ऊंचाई ज्ञात कीजिए। (NCERT प्रश्नावली 9.1 ,प्रश्न संख्या 4)
मैं इस सवाल को बनाऊंगा नहीं बल्कि सवाल को बनाने का तरीका बताऊंगा ताकि इससे रिलेटेड भी सवाल आये तो आप उसे आराम से बना ले। इस सवाल में सबसे पहले जो बोला गया है उसे समझना है।
- प्रश्न में कह रहा है, भूमि के एक बिंदु से। सबसे पहले एक बिंदु बनाएंगे और वह बिंदु हवा में नहीं धरती पर मान के चलेंगे।
- आगे प्रश्न में कहा जा रहा है मीनार के पाद बिंदु से, पाद का मतलब होता है पैर (मीनार के निचला बिंदु ) 30 मीटर की दूरी पर है। मतलब हम जो भूमि पर एक बिंदु खिंचा है वह मीनार के पाद (पैर) बिंदु से 30 मीटर दूरी पर है।
- आगे कहा जा रहा है, मीनार के शिखर का उन्नयन कोण 30 डिग्री है। मतलब हम जो बिंदु बनाये हैं, अगर उस बिंदु से मीनार के शिखर को मिलाएंगे तो मेरे मनाएंगे बिंदु पर मीनार के शिखर और मीनार के पाद से लगे रेखा के द्वारा एक कोण बनेगा । उसी कोण का माप 30 डिग्री है।
- प्रश्न का लास्ट भाग कह रहा है मीनार की ऊंचाई ज्ञात करें ?
जैसे-जैसे सवाल में कहा गया है उसी तरीके से सोचे तो एक समकोण बनाता है। अब इस समकोण में आधार का माप दिया गया है। और आधार और कर्ण से लगने वाली रेखा से बना कोण का भी माप दिया गया है। अब सूत्र का उपयोग करते हुए लम्ब निकाल लेंगे।
यहाँ हमें सूत्र याद करना पड़ेगा और सोचना पड़ेगा कि कौन-सा सूत्र लागू होगा। यहाँ इस प्रश्न में लम्ब और आधार के अनुपात वाले सूत्र का उपयोग होगा। (लम्ब /आधार ) = tanø
tanø = लम्ब/आधार
tan30°= लम्ब/30
30 × tan30° = लम्ब
लम्ब = 30 × tan30°
इसको हल करके आप मीनार का लम्ब निकाल सकते हैं।
Q2. 1.5m लंबा एक लड़का 30m ऊंचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊंचे भवन की ओर जाता है तब उसकी आंख से भवन के शिखर का उन्नयन कोण 30 डिग्री से 60 डिग्री हो जाता है। बताइए कि वह भवन की ओर कितनी दूर तक चलकर गया है। (NCERT प्रश्नावली 9.1 ,प्रश्न संख्या 6)
यह सवाल बहुत ही सुंदर है और बहुत ही हल्का है। सबसे पहले इस सवाल को समझने की कोशिश कीजिए। उसके बाद चित्र के माध्यम से इस सवाल को समझिए। उसके बाद सवाल बनाने की कोशिश कीजिए। अगर सवाल समझ में नहीं आया तो सवाल को मत बनाइए। क्योंकि इसका कुछ फायदा होने वाला नहीं है।
सवाल किसी न किसी विधि से आपको समझना ही पड़ेगा। अगर मेरे लिखे से भी बिल्कुल भी समझ नहीं आ रहा है तो आप हमें नीछे कमेंट के माध्यम से बताइए। हम इसे वीडियो की मध्यम से सवाल को समझाएंगे। एक सवाल अगर आप अच्छी तरह से समझ गए तो आप इस चैप्टर के कोई भी सवाल को हल कर सकते हैं।
आप मुझे YouTube , Telegram पर भी फ्लो कर लीजिए।
Class 10 Maths Topic (थ्योरी )
- Chapter 1: वास्तविक संख्या (Real Numbers)
- Chapter 2: बहुपद (Polynomials)
- Chapter 3: दो चर वाले रैखिक युग्म (Pair of Linear Equations in Two Variables)
- Chapter 4: द्विघात समीकरण (Quadratic Equations)
- Chapter 5: समांतर श्रेढ़ियाँ (Arithmetic Progressions)
- Chapter 6: त्रिभुज (Triangles)
- Chapter 7: निर्देशांक ज्यामिति (Coordinate Geometry)
- Chapter 8: त्रिकोणमिति का परिचय (Introduction to Trigonometry)
- Chapter 9: त्रिकोणमिति के कुछ अनुप्रयोग (Some Applications of Trigonometry)
- Chapter 10: वृत (Circles)
- Chapter 11: रचनाएँ (Constructions)
- Chapter 12: वृतों से संबंधित क्षेत्रफल (Areas Related to Circles)
- Chapter 13: पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes)
- Chapter 14: सांख्यकी (Statistics)
- Chapter 15: प्रायिकता (Probability)
व्यापार नॉलेज :-
1.शेयर मार्केट क्या होता है (Stock Market)
2.ट्रेडिंग कैसे करें और क्या होता है (Trading)
3. म्यूच्यूअल फंड क्या होता है (Mutual Fund)